Category: Numerical Analysis

New Jacobi Polynomials Application January 8, 2024, by James Pate Williams, Jr.

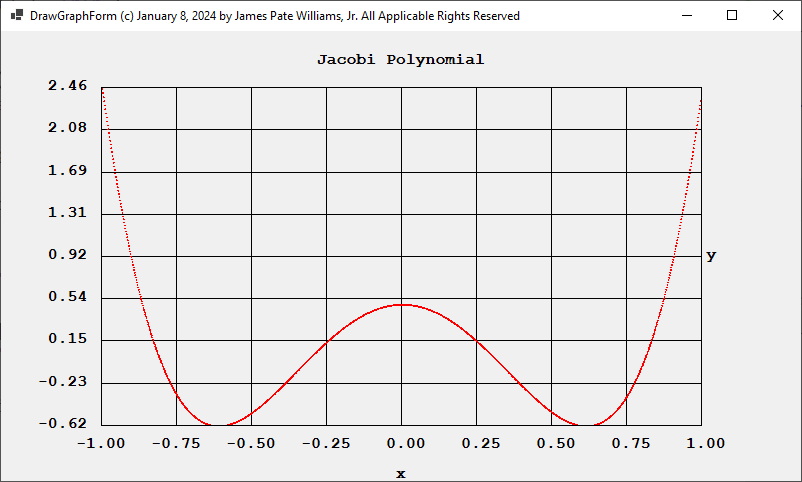
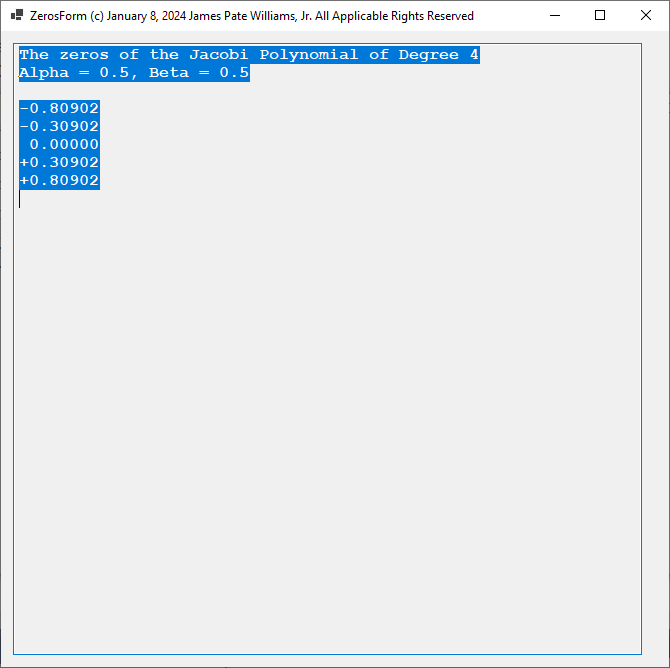
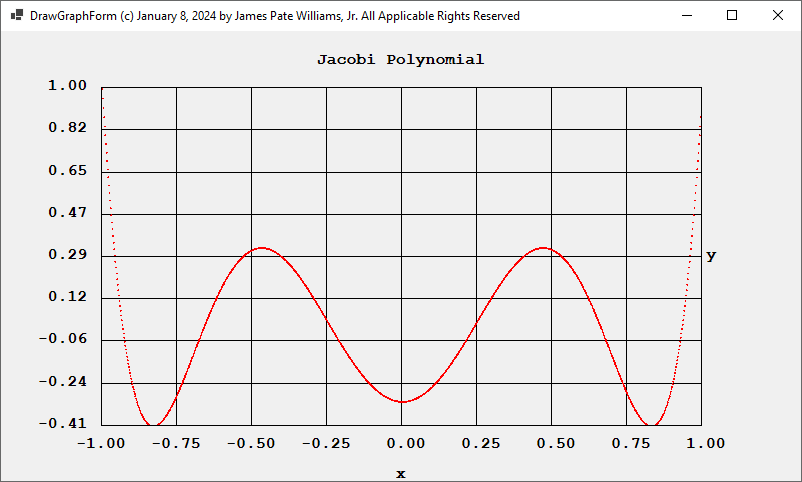
The two primary references used to create my application were: “A Numerical Library in C for Scientists and Engineers” by H. T. Lau and the following website: https://en.wikipedia.org/wiki/Jacobi_polynomials.

Using the Jacobi parameters alpha = 0 and beta = 0, we have the Legendre polynomials for degrees 4 and 6 and their associated roots:

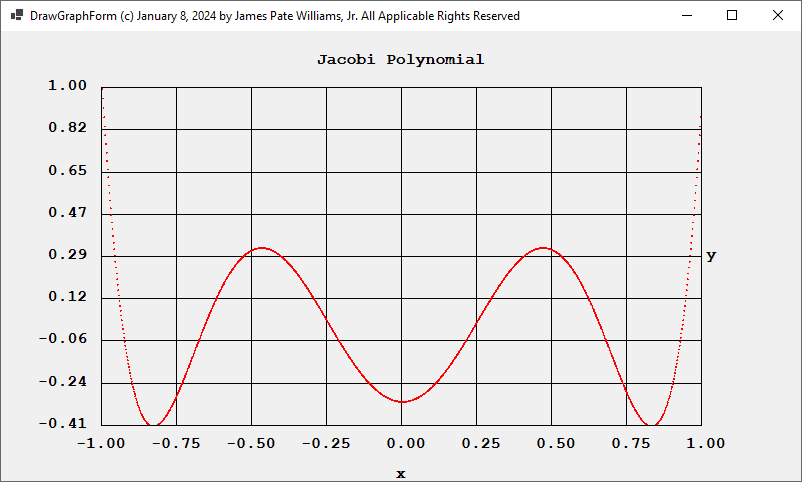
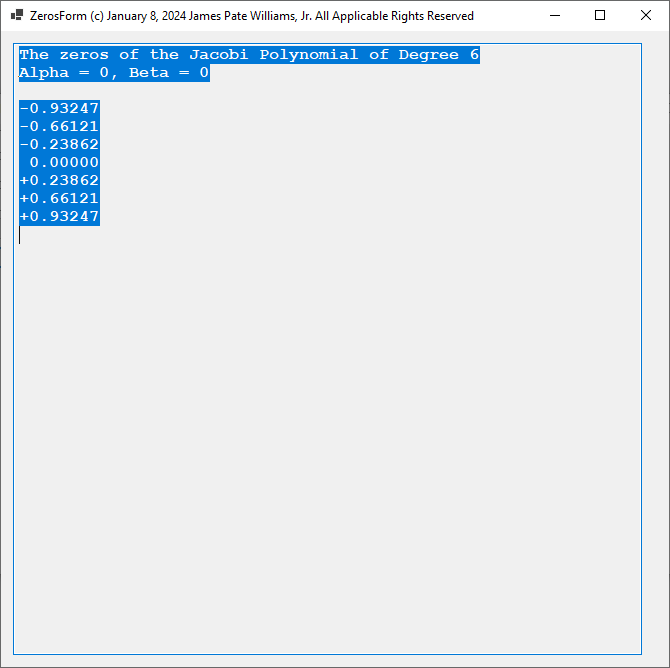
Using alpha = 0.5 and beta= 0.5 we obtain for degrees 4 and 6:

Electron Probability Distribution Function Etc. (c) James Pate Williams, Jr. December 2023

electron-probability-distribution-function-etcDownload

Some Helium Coulomb Integrals over Six Dimensions by James Pate Williams, Jr. Source Code in C++ Development over December 15 – 16, 2023

some-helium-coulomb-integrals-1Download

Revised Translated Source Code from May 15, 2015, by James Pate Williams, Jr.

revisited-with-source-code-translation-and-revisionDownload

New and Corrected Ground State Energy Numerical Computation for the Helium Like Atom (Atomic Number 2) by James Pate Williams, Jr.

approximate-solution-of-the-schrodinger-equation-for-the-helium-atom-1Download
new-variational-treatment-of-the-helium-like-atom-revisedDownload

A New Calculus of Variations Solution of the Schrödinger Equation for the Lithium Like Atom’s Ground State Energy

This computation took a lot longer time to reach a much better solution than my previously published result.

new-variational-solution-for-the-lithiumDownload

A Calculus of Variations Solution to the Quantum Mechanical Schrödinger Wave Equation for the Lithium Like Atom (Atomic Number Z = 3) by James Pate Williams, Jr.

variational-solution-for-the-lithiumDownload