The first solution is from the textbook, Elementary Numerical Analysis: An Algorithmic Approach (c) 1980 by S. D. Conte and Carl de Boor. I translated the FORTRAN code to vanilla C using Visual Studio 2019 Community Version. The second solution is from Boundary Value Problems Second Edition (c) 1979 by David L. Powers. It solves a simple second order linear ordinary differential equation using the finite element difference equation method.
Category: Numerical Analysis
Blog Entry for Early Morning Friday, May 31, 2024, Solutions of a Second Order Self-Adjoint Ordinary Differential Equation by Three Methods
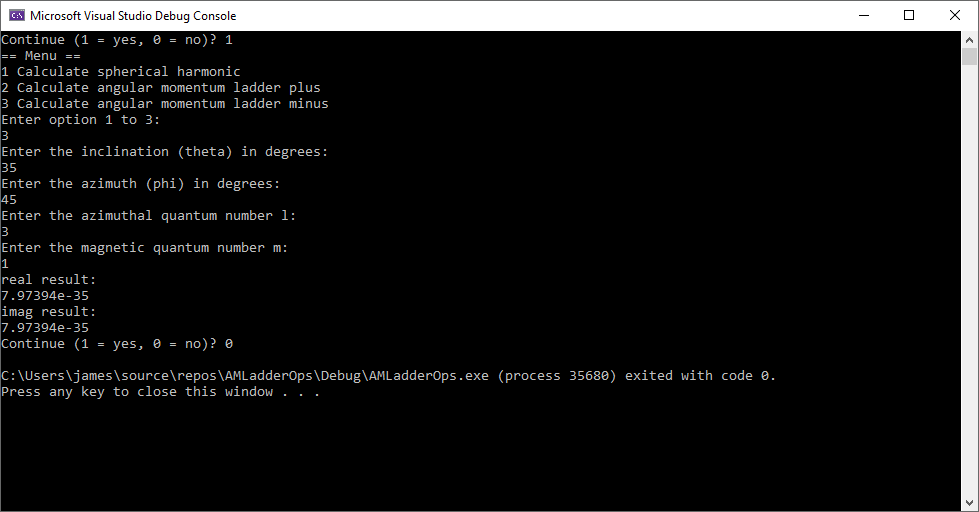
Quantum Mechanical Angular Momentum Ladder Operators by James Pate Williams, Jr. Copyright Thursday, May 23, 2024, All Applicable Rights Reserved
A Few Problems from Schiff Chapter 6 (c) May 19-20, 2024, by James Pate Williams, Jr.
Text and Exercise from “Boundary Value Problems Second Edition” by David L. Powers in Progress (c) Wednesday, April 17, 2024, James Pate Williams, Jr.
Solution of the Laplace (Potential) Equation on a Two-Dimensional Square via Finite Differences
Solution of the One-Dimensional Heat Equation for a Rod Using Finite Differences by James Pate Williams, Jr. Created on Wednesday April 3, 2024
Undamped Mass-Spring Eigenvalue – Eigenvector Problem by James Pate Williams, Jr. (c) Monday April 1, 2024
We extend the results of the following website:
The five masses in the problem have a maximum value of 8. The six springs have a maximum value of 4 for their Hooke’s coefficients. The first 5 by 5 matrix is the inverse mass matrix, the second matrix is the Hooke’s coefficient 5 by 5 matrix, the third 5 by 5 matrix is the product of the inverse mass matrix times the Hooke’s coefficient matrix. The final row vector is the eigenvalue vector.
Numerical Explorations 