Category: Quadratic Formula
Blog Entry (c) Saturday August 31, 2024, by James Pate Williams, Jr. An Elementary School Problem Found Online
Solve for a real root of the equation
f(x)=log6l(5+x)+log6l(x)=0
First we test our log6l(x) function
log6l(12) = 1.386853
log6l(36) = 2.000000
x = 0.1925824036
f = 0.0000000000
Blog Entry (c) Friday August 30, 2024, by James Pate Williams, Jr. Another Simple Math Problem
We use an evolutionary hill-climber and the solution of the quadratic equation to solve the easy problem below:
Solution of f(a,x)=sin(sqrt(ax-x^2))=0
Subject to the constraint x+y=100
Where x and y are the two roots of
g(a,x)=ax-x^2-n*n*pi*pi=0
and n=15
a = 100.347888933988
x = 32.947113268776
y = 67.400775665213
g = 0.000000000000
s = 100.347888933988
runtime in seconds = 43.730000
Blog Entry (c) Tuesday, July 23, 2024, by James Pate Williams, Jr. Mueller’s Method for Finding the Complex and/or Real Roots of a Complex and/or Real Polynomial
I originally implemented this algorithm in FORTRAN IV in the Summer Quarter of 1982 at the Georgia Institute of Technology. I was taking a course named “Scientific Computing I” taught by Professor Gunter Meyer. I made a B in the class. Later in 2015 I re-implemented the recipe in C# using Visual Studio 2008 Professional. VS 2015 did not have support for complex numbers nor large integers. In December of 2015 I upgraded to Visual Studio 2015 Professional which has support for big integers and complex numbers. I used Visual Studio 2019 Community version for this project. Root below should be function.
Degree (0 to quit) = 2
coefficient[2].real = 1
coefficient[2].imag = 0
coefficient[1].real = 1
coefficient[1].imag = 0
coefficient[0].real = 1
coefficient[0].imag = 0
zero[0].real = -5.0000000000e-01 zero[0].imag = 8.6602540378e-01
zero[1].real = -5.0000000000e-01 zero[1].imag = -8.6602540378e-01
root[0].real = 0.0000000000e+00 root[0].imag = -2.2204460493e-16
root[1].real = 3.3306690739e-16 root[1].imag = -7.7715611724e-16
Degree (0 to quit) = 3
coefficient[3].real = 1
coefficient[3].imag = 0
coefficient[2].real = 0
coefficient[2].imag = 0
coefficient[1].real = -18.1
coefficient[1].imag = 0
coefficient[0].real = -34.8
coefficient[0].imag = 0
zero[0].real = -2.5026325486e+00 zero[0].imag = -8.3036679880e-01
zero[1].real = -2.5026325486e+00 zero[1].imag = 8.3036679880e-01
zero[2].real = 5.0052650973e+00 zero[2].imag = 2.7417672687e-15
root[0].real = 0.0000000000e+00 root[0].imag = 1.7763568394e-15
root[1].real = 3.5527136788e-14 root[1].imag = -1.7763568394e-14
root[2].real = 2.8421709430e-14 root[2].imag = 1.5643985575e-13
Degree (0 to quit) = 5
coefficient[5].real = 1
coefficient[5].imag = 0
coefficient[4].real = 2
coefficient[4].imag = 0
coefficient[3].real = 3
coefficient[3].imag = 0
coefficient[2].real = 4
coefficient[2].imag = 0
coefficient[1].real = 5
coefficient[1].imag = 0
coefficient[0].real = 6
coefficient[0].imag = 0
zero[0].real = -8.0578646939e-01 zero[0].imag = 1.2229047134e+00
zero[1].real = -8.0578646939e-01 zero[1].imag = -1.2229047134e+00
zero[2].real = 5.5168546346e-01 zero[2].imag = 1.2533488603e+00
zero[3].real = 5.5168546346e-01 zero[3].imag = -1.2533488603e+00
zero[4].real = -1.4917979881e+00 zero[4].imag = 1.8329656063e-15
root[0].real = 8.8817841970e-16 root[0].imag = 4.4408920985e-16
root[1].real = -2.6645352591e-15 root[1].imag = -4.4408920985e-16
root[2].real = 8.8817841970e-16 root[2].imag = 1.7763568394e-15
root[3].real = 3.4638958368e-14 root[3].imag = -1.4210854715e-14
root[4].real = 8.8817841970e-16 root[4].imag = 2.0710031449e-14
A Few Problems from Schiff Chapter 6 (c) May 19-20, 2024, by James Pate Williams, Jr.
Quadratic, Cubic, and Quartic Python Equation Solver by James Pate Williams Jr
Back in 2015 I created a C# application to solve quadratic, cubic, and quartic equations which are of degrees 2, 3, and 4, respectively. Yesterday I successfully translated the C# to the Python console. I bench-marked my computer programs against the online calculators on the following website:
Cubic equation Calculator – High accuracy calculation (casio.com)
Quartic equation Calculator – High accuracy calculation (casio.com)
Here are my resulting Python outputs:


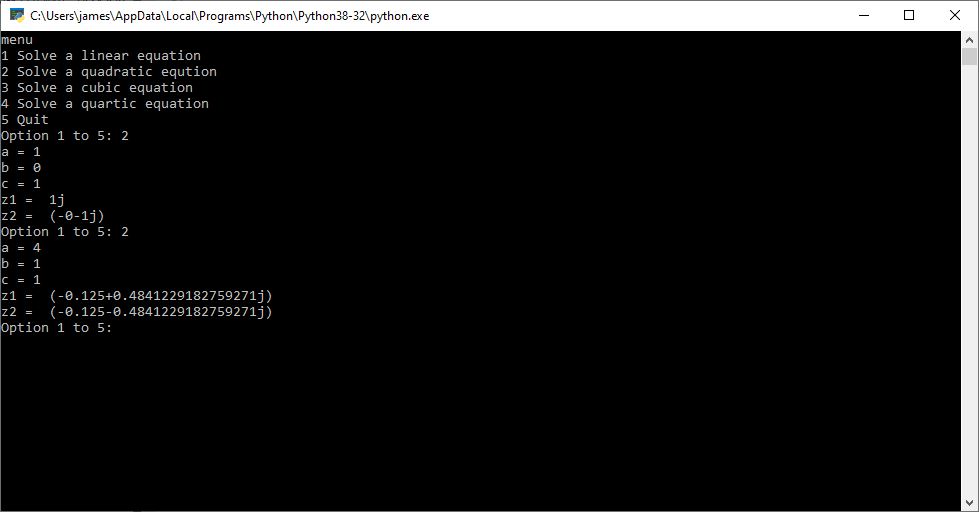

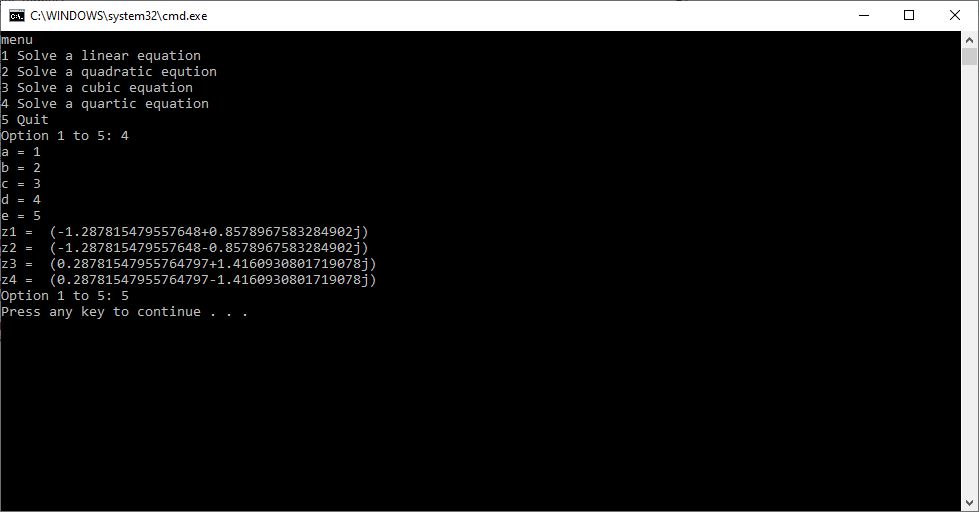
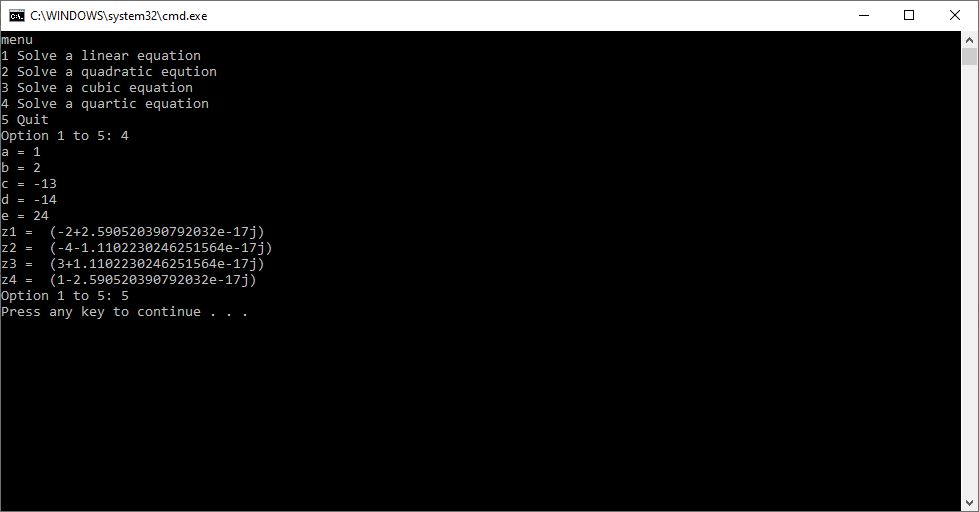
Newton’s Second Law of Motion an Introduction by James Pate Williams, Jr.

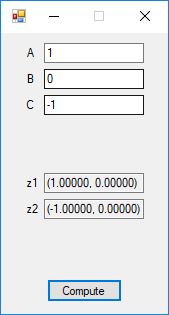
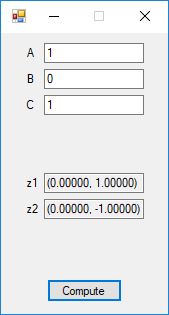
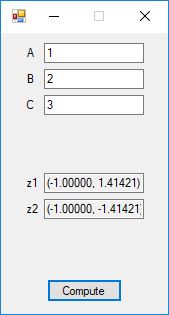
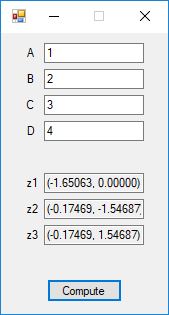
Roots of Small Degree Polynomials with Real Coefficients by James Pate Williams, BA, BS, MSwE, PhD
We designed and implemented quadratic formula, cubic formula, and quartic formula solvers using the formulas in the Wikipedia articles:
https://en.wikipedia.org/wiki/Quadratic_formula
https://en.wikipedia.org/wiki/Cubic_function
https://en.wikipedia.org/wiki/Quartic_function
We tested our C# implementation against:
https://keisan.casio.com/exec/system/1181809415
http://www.wolframalpha.com/widgets/view.jsp?id=3f4366aeb9c157cf9a30c90693eafc55
https://keisan.casio.com/exec/system/1181809416
Here are screenshots of the C# application:
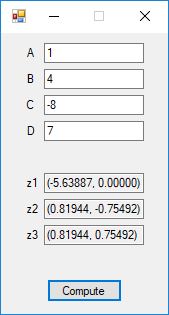
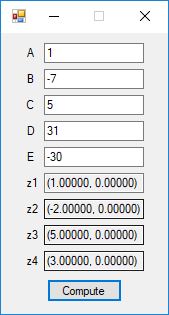
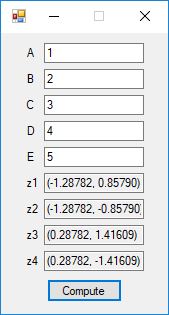
C# source code files for the application: