Category: Root Finding Algorithms

function exp(-x) - sin(0.5 * pi * x)
The interval found by bisection is:
a = +0.4435735341  b = +0.4435735341
bisection # iterations = 50
The root by regula falsi:
x = +0.4435735341  f(x) = -0.0000000000
regula falsi # iterations = 8
The root by the secant method:
x = +0.4435735341  f(x) = +0.0000000000
secant method # iterations = 9
The root by Newton's Method:
x = +0.4435735341  f(x) = -0.0000000000
Newton's Method # iterations = 6

D:\roots\x64\Release\roots.exe (process 28152) exited with code 0 (0x0).
Press any key to close this window . . .

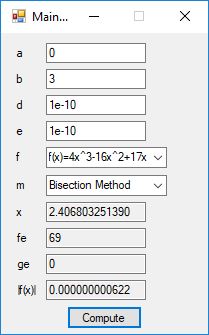
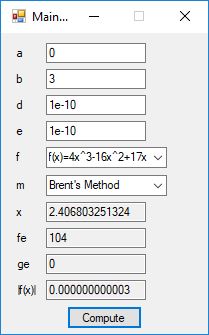
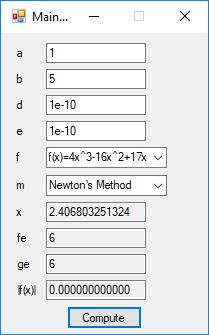
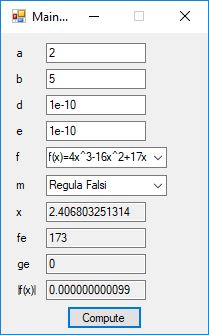
#include <math.h>
#include <stdio.h>

typedef double real;

static real f(real x)
{
	double pi2 = 2.0 * atan(1.0);
	return(exp(-x) - sin(pi2 * x));
}

static real g(real x)
{
	double pi2 = 2.0 * atan(1.0);
	return(-exp(-x) - pi2 * cos(pi2 * x));
}

static int bisection(
	real(*f)(real), real* a, real* b, real xtol, int* flag)
{
	real error, fa, fm, xm;
	int n = 0;

	fa = (*f)(*a);
	if (fa * (*f)(*b) > 0.0)
	{
		*flag = -1;
		return(n);
	}
	error = fabsl(*b - *a);
	while (error > xtol)
	{
		n++;
		error *= 0.5;
		if (error <= xtol)
		{
			*flag = 0;
			return(n);
		}
		xm = 0.5 * (*a + *b);
		if (xm + error == xm)
		{
			*flag = 1;
			return(n);
		}
		fm = (*f)(xm);
		if (fa * fm > 0.0)
		{
			*a = xm;
			fa = fm;
		}
		else
			*b = xm;
	}
	*flag = 2;
	return(n);
}

static int regula(
	real (*f)(real), real a, real b, real xtol,
	real ftol, int ntol, real* w, int* flag)
{
	int n = 0;
	real fa, fb, fw, signfa, prvsfw;

	fa = f(a);
	if (fa >= 0.0) signfa = +1.0; else signfa = -1.0;
	fb = f(b);
	if (signfa * fb >= 0.0)
	{
		*flag = -1;
		return n;
	}
	*w = a;
	fw = fa;
	for (n = 0; n <= ntol; n++)
	{
		if (fabs(a - b) <= xtol)
		{
			*flag = 0;
			return n;
		}
		if (fabs(fw) <= ftol)
		{
			*flag = 1;
			return n;
		}
		*w = (fa * b - fb * a) / (fa - fb);
		if (fw >= 0.0) prvsfw = +1.0; else prvsfw = -1.0;
		fw = f(*w);
		if (signfa * fw > 0.0)
		{
			a = *w;
			fa = fw;
			if (fw * prvsfw > 0.0) fb = 0.5 * fb;
		}
		else
		{
			b = *w;
			fb = fw;
			if (fw * prvsfw > 0.0) fa = 0.5 * fa;
		}
	}
	*flag = 2;
	return n;
}

static int secantMethod(
	real(*f)(real), real xtol, real ftol,
	int ntol, real xm1, real x0, real* w)
{
	real fm1 = f(xm1), f0 = f(x0);
	real df = fabs(fm1 - f0), f1 = 0.0;
	real dx = fabs(xm1 - x0), x1 = 0.0;
	int n = 0;

	while (n < ntol && df > ftol && dx > xtol)
	{
		x1 = (f0 * xm1 - fm1 * x0) / (f0 - fm1);
		f1 = f(x1);
		df = fabs(f(x1) - f0);
		dx = fabs(x1 - x0);
		fm1 = f0;
		f0 = f1;
		xm1 = x0;
		x0 = x1;
		n++;
	}

	*w = x1;
	return n;
}

static int NewtonsMethod(
	real(*f)(real), real(*g)(real),
	real xtol, real ftol, int ntol,
	real* w)
{
	// f is the function
	// g is the function's derivative
	// xtol is root's tolerance
	// ftol is the function's tolerance
	// ntol is the maximum # of iterations
	real f1 = 0.0, g1 = 0.0, x0 = *w, x1 = 0.0;
	real f0 = f(x0), g0 = g(x0);
	real deltaX = DBL_MAX, deltaF = DBL_MAX;
	int n = 0;

	while (n < ntol && deltaX > xtol && deltaF > ftol)
	{
		x1 = x0 - f0 / g0;
		f1 = f(x1);
		g1 = g(x1);
		deltaX = fabs(x1 - x0);
		deltaF = fabs(f1 - f0);
		f0 = f1;
		g0 = g1;
		x0 = x1;
		n++;
	}

	*w = x1;
	return n;
}

int main(void)
{
	int flag = 0, ntol = 0;
	real a0 = 0, b0 = 0, ftol = 0, w1 = 0, w2 = 1.0;
	real a1 = 0, b1 = 0, w3 = 0, xtol = 0;

	a0 = 0.0;
	b0 = 1.0;
	ntol = 128;
	ftol = 1.0e-15;
	xtol = 1.0e-15;
	int its1 = bisection(f, &a0, &b0, xtol, &flag);
	a1 = 0.0;
	b1 = 1.0;
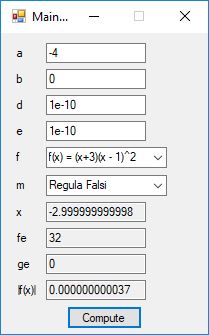
	int its2 = regula(f, a1, b1, xtol, ftol, ntol, &w1, &flag);
	int its3 = secantMethod(f, ftol, xtol, ntol, 0.0, 1.0, &w2);
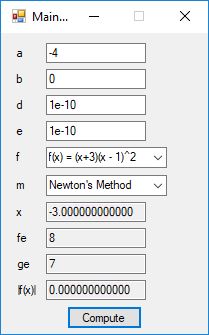
	int its4 = NewtonsMethod(f, g, xtol, ftol, ntol, &w3);
	printf("function exp(-x) - sin(0.5 * pi * x)\n");
	printf("The interval found by bisection is:\n");
	printf("a = %+13.10lf  b = %+13.10lf\n", a0, b0);
	printf("bisection # iterations = %ld\n", its1);
	printf("The root by regula falsi:\n");
	printf("x = %+13.10lf  f(x) = %+13.10lf\n", w1, f(w1));
	printf("regula falsi # iterations = %ld\n", its2);
	printf("The root by the secant method:\n");
	printf("x = %+13.10lf  f(x) = %+13.10lf\n", w2, f(w2));
	printf("secant method # iterations = %ld\n", its3);
	printf("The root by Newton's Method:\n");
	printf("x = %+13.10lf  f(x) = %+13.10lf\n", w2, f(w3));
	printf("Newton's Method # iterations = %ld\n", its4);
	return(0);
}