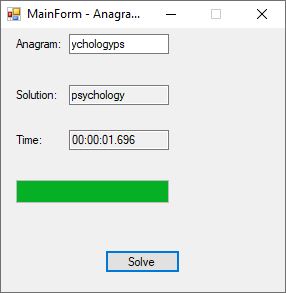
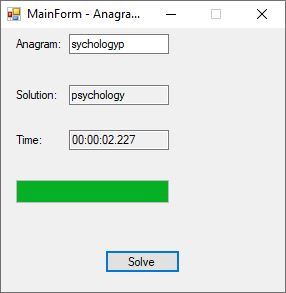
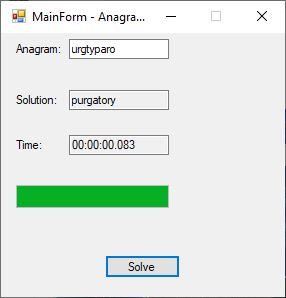
C# Computer Programming Language – Page 10

Anagrams and Their Computer Solution by James Pate Williams, Jr., BA, BS, MSwE, PhD

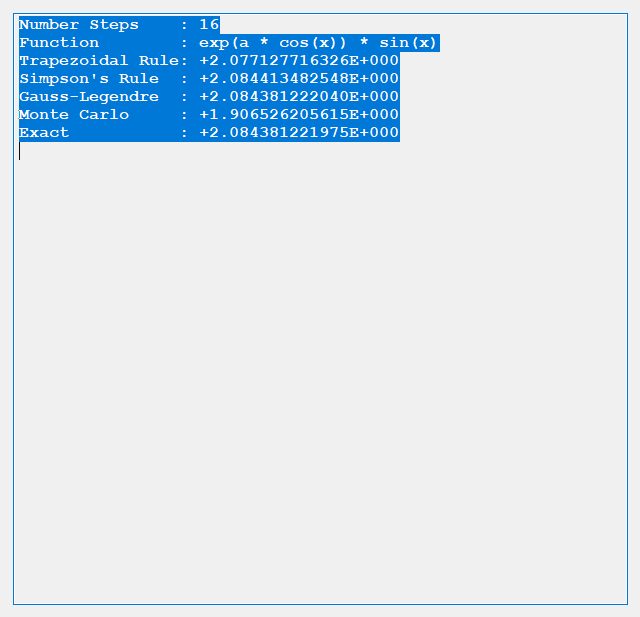
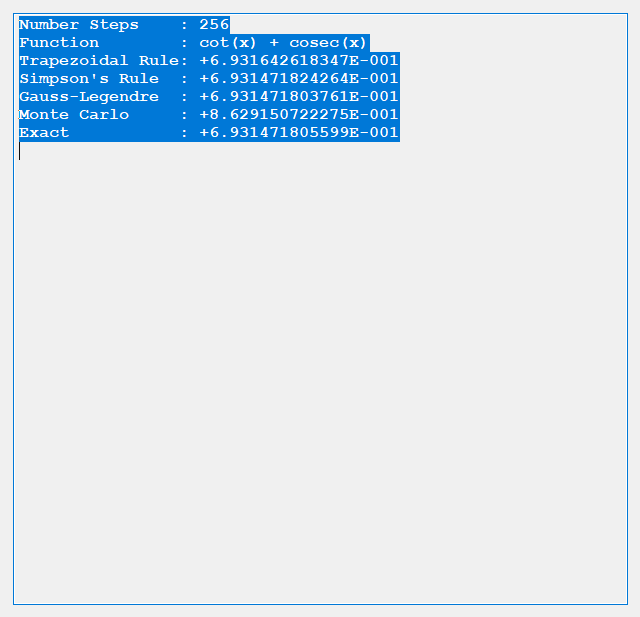
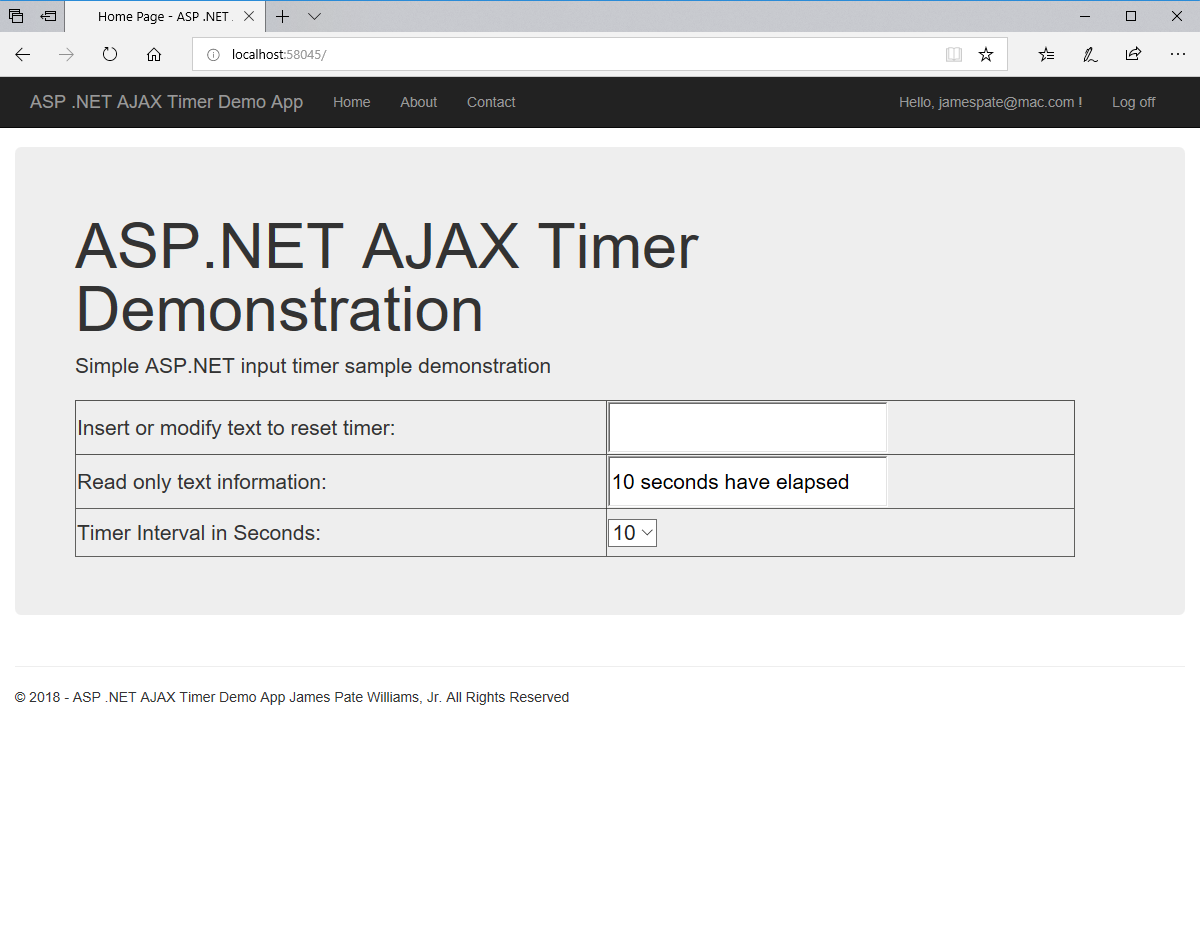
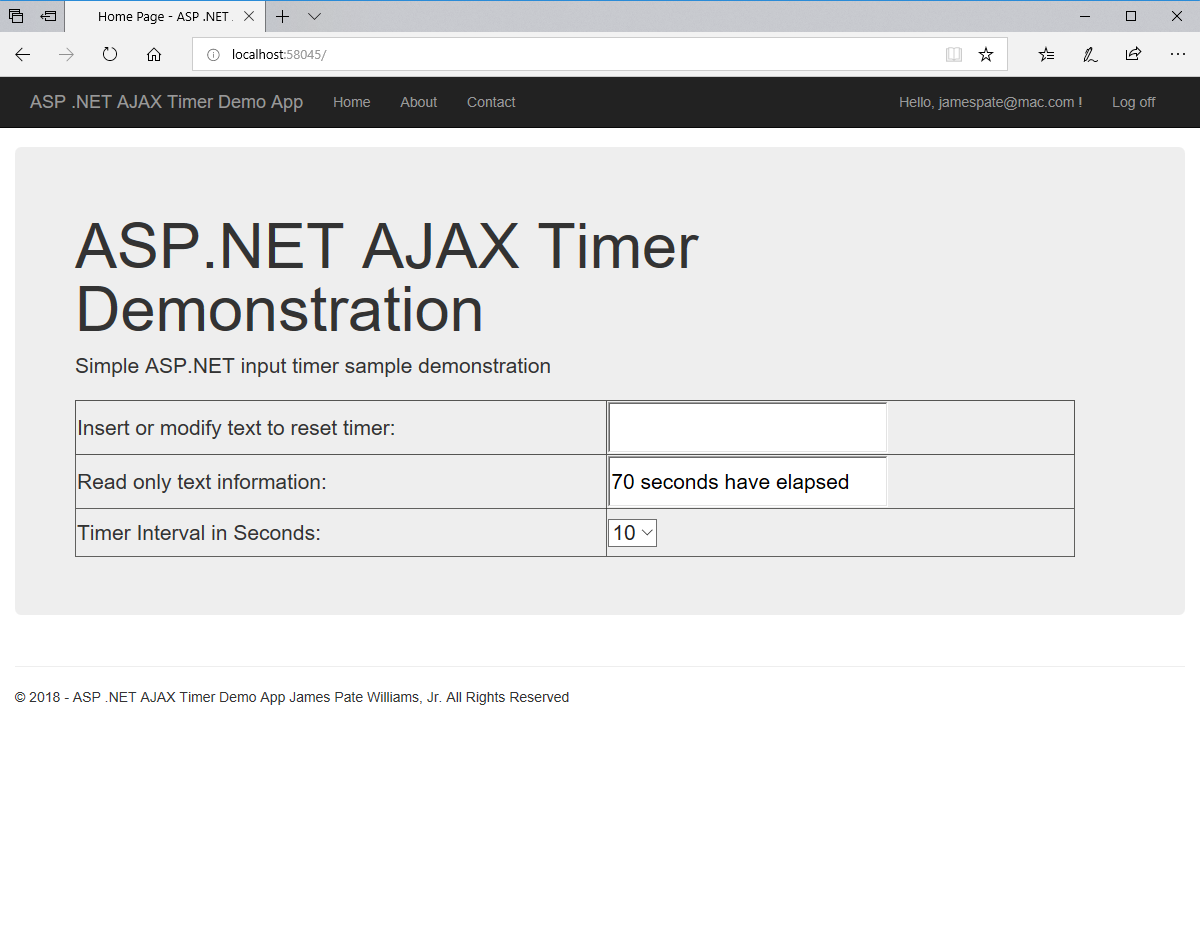
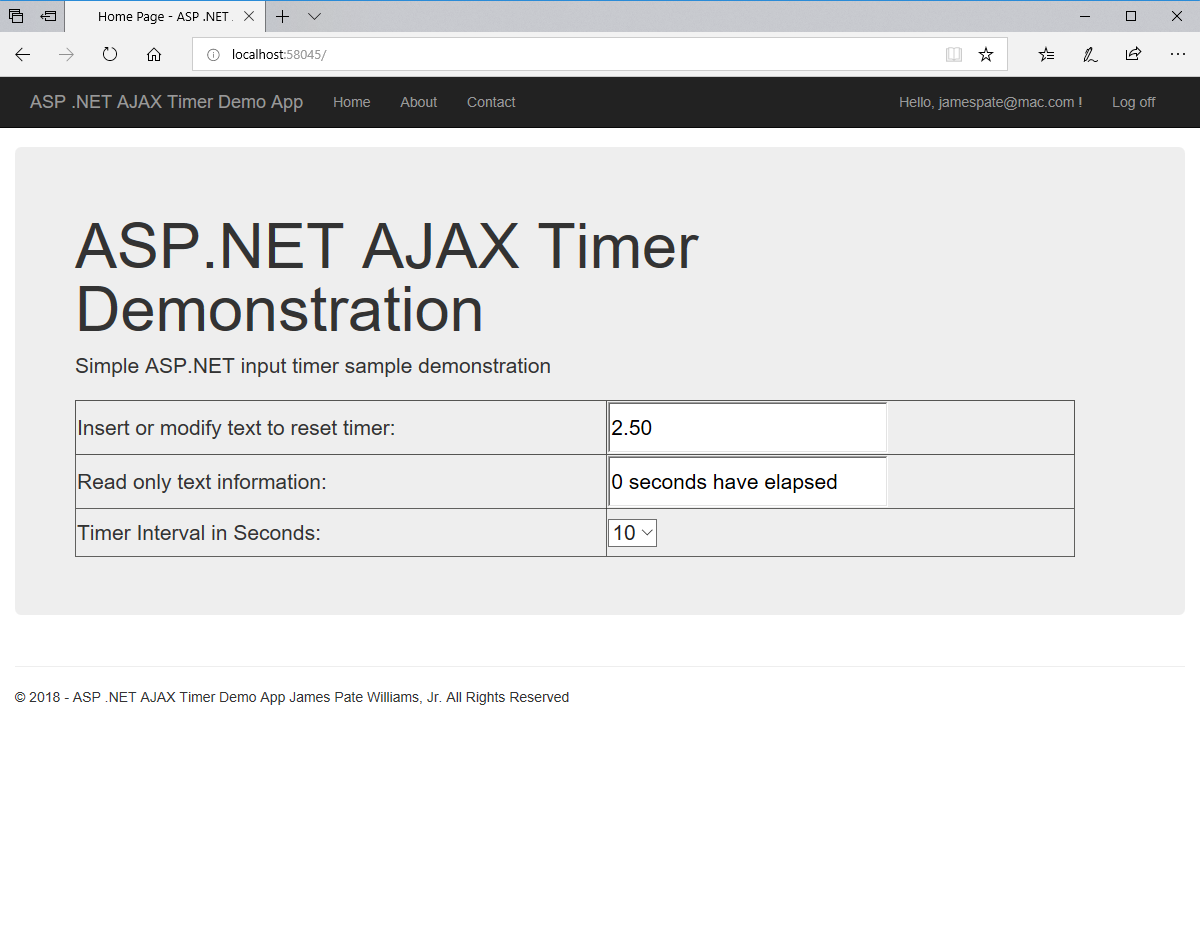
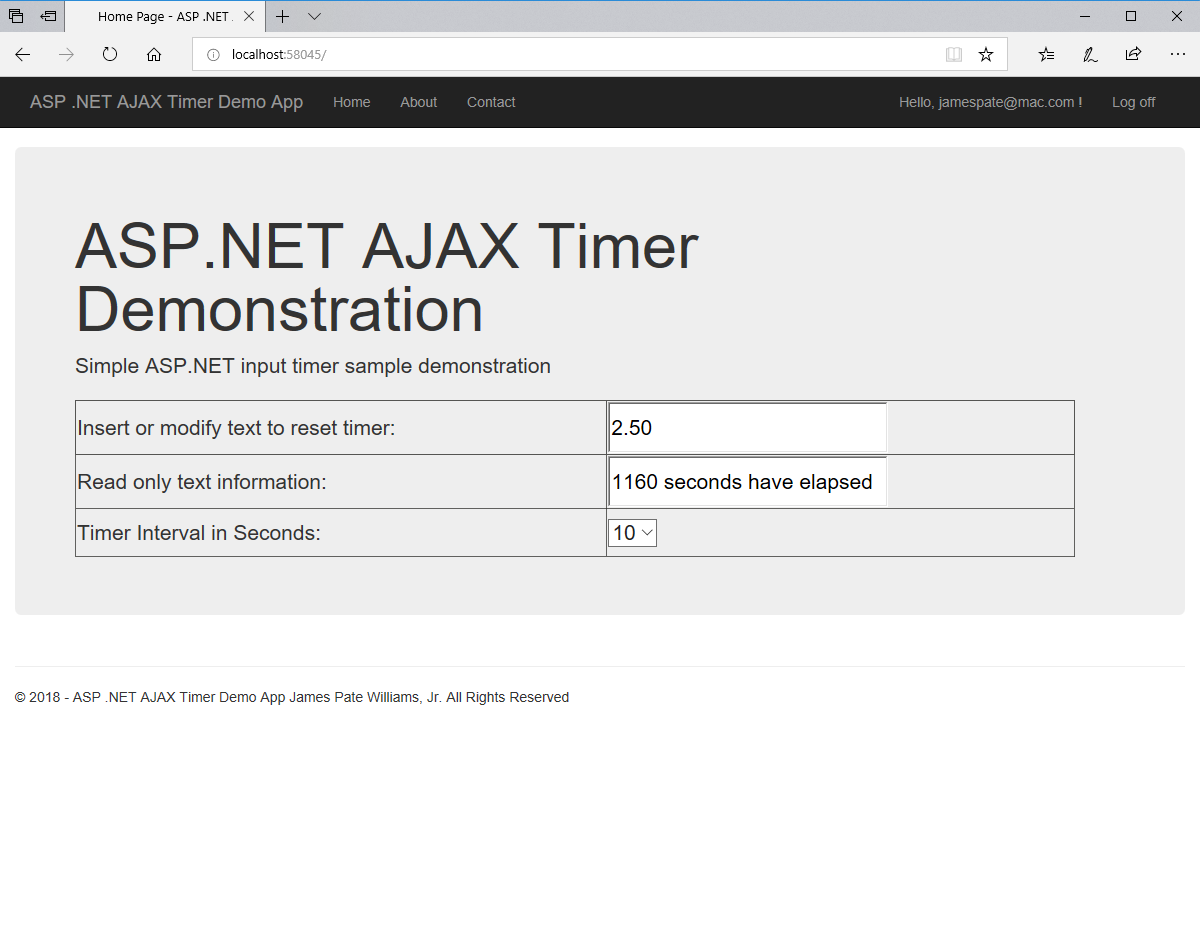
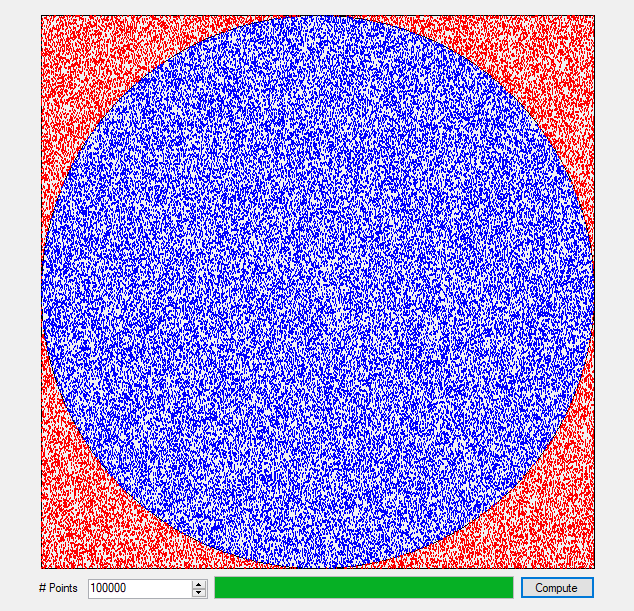
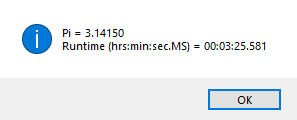
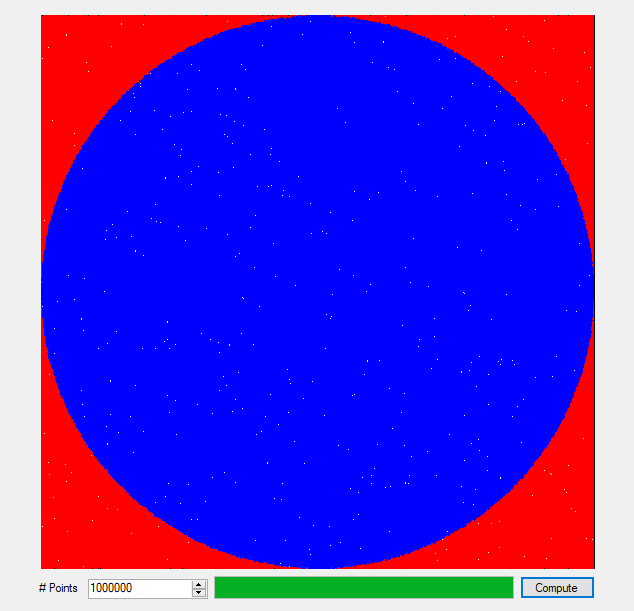
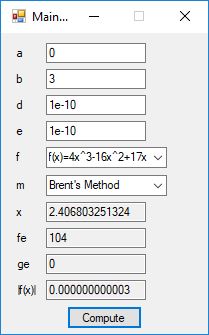
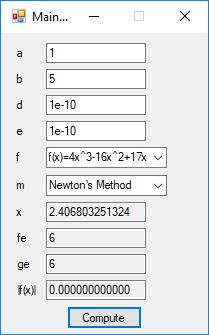
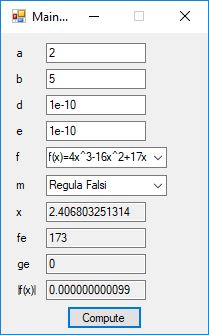
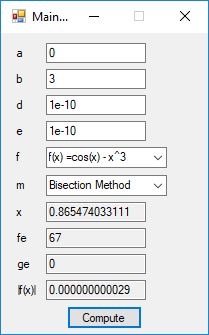
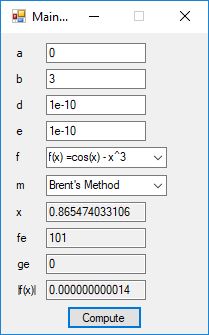
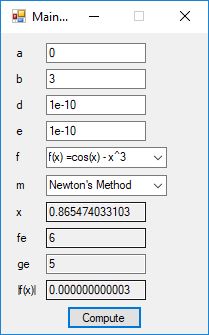
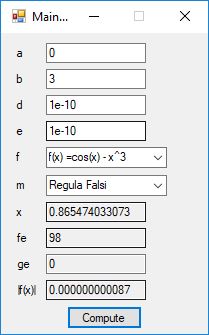
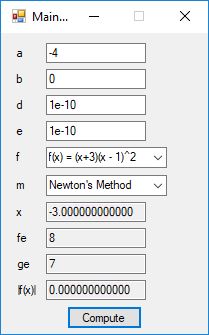
An anagram is also known as a word jumble. You take a word and apply a permutation to the word to get an alphabetic jumble of the word. A permutation of three distinct characters is based on three index permutation table:

123 132 213 231 312 321.

So, the scrambling of the word “THE” is as follows:

THE TEH HTE HET ETH EHT.

As you can see there are n-factorial permutations of n objects.

0! = 1

1! = 1

2! = 2 * 1 = 2

3! = 3 * 2 * 1 = 6

4! = 4 * 3 * 2 * 1 = 4 * 3! = 24

Etc. Several years ago I created a program to solve single word anagrams of length less than or equal about a dozen.

12! = 479,001,600

This is about the limit of finding all the permutations of up to length twelve on a desktop computer. The algorithm is extremely easy to understand and implement. First find a suitable list of English words and if the list is unsorted then sort the list alphabetically in ascending order. Hash the dictionary words using a hash table of length 128 * 128 + 128 = 16,512 elements. The dictionary I used has 152,512 words so there are hash table collisions. The hash value is computed using the first three characters of the word in ASCII (7-bit) encoding. Then for each permutation of the anagram a hash value is computed and if the current permutation is found in the hash table the word associated with the hash table entry is returned and the algorithm is finished.

Baseball Ballistics by James Pate Williams, Jr., BS, BS, MSwE, PhD

There are analytic equations that are applicable to the trajectory of a batted or thrown baseball:

Click to access 04-LAJPE-782_Chudinov.pdf

I created a C# application to test the preceding equations against numerical methods of calculating the trajectory of a baseball. The baseball has an initial velocity of 90 miles per hour and an angle of inclination of 20 degrees. The classical model certainly overestimates the trajectory.

Siacci’s Method by James Pate Williams, Jr. BA, BS, MSwE, PhD

Siacci’s Method Chapter 5 and Appendix A of “Exterior Ballistics, 1935” by Lieutenant Commander Ernest Edward Herrmann of the United States Naval Academy. This is an approximate technique for solving exterior ballistics trajectories with between 12 to 15 degrees of elevation. The artillery is the 16 inch / 50 caliber rifled guns of the Iowa class of fast battleships (BB-61 USS Iowa, BB-62 USS New Jersey, BB-63 USS Missouri, and BB-64 USS Wisconsin).

Range Table 0 Range Table 2 Range Table 1 ExteriorBallisticsRK5 Main Form

My Near-Term Agenda by James Pate Williams, Jr. BA, BS, MSwE, PhD

Merry Christmas to all you devout Christians. I am not one of you. I am about to embark on a mission to carefully annotate with open source C# computer code my copy of “Exterior Ballistics, 1935” by Professor Ernest Edward Herrmann of then the United States Naval Academy at Annapolis, Maryland. This book set the standard for naval gunnery in World War II. Of course, our navy and especially our battle-wagons had the largest rifled artillery of any United States service. The 105 mm = 105 mm / 25.4 mm / inch = 4.13 inches, 120 mm / 25.4 mm / inch = 4.72 inches, and 155 mm / 25.4 mm / inch = 6.10 inch of our excellent United States Army and United States Marine Corps (semper fidelis) are puny in comparison to the mighty 8, 10, 12, 14, and finally 16 inch mostly rifled artillery of our incredible navy’s cruisers, dreadnoughts, and battleships of the World War I and World War II era ships. Even a destroyer of the USN Fletcher class had 5-inch (127 mm) / 38 caliber rifled artillery which had a 5 inch * 38 = 190-inch barrel length. Our mightiest naval artillery was, of course, my favorite the mighty 16 inch (406.4 mm) / 50 caliber rifles that had a barrel length of 16 * 50 inches = 800 inches = 66.6 feet!

Thanks,

James Pate Williams, Jr.

Bachelor of Arts Chemistry LaGrange College 1979

Bachelor of Science Computer Science LaGrange College 1994

Master of Software Engineering Auburn University 2000

Doctor of Philosophy Computer Science Auburn University 2005

Gratis Open Source Computer Software Developer Since Summer 1978

1980 – 1983 Graduate Work in Chemistry and Mathematics at Georgia Tech

A Current Website I developed for my friends Wesley “Wes” and Missy Cochran:

http://thecochrancollection.com/Home

MyLabRadarCompanion by James Pate Williams, Jr. BA, BS, MSwE, PhD

This slideshow requires JavaScript.

Four Techniques for One Dimensional Riemann Definite Integration by James Pate Williams, Jr. BA, BS, MSwE, PhD

The four methods considered in this study are as follows:

Trapezoidal Rule
Simpson’s Rule
Gauss-Legendre Quadrature
Monte Carlo Method

The trapezoidal rule requires (n + 2) function evaluations, n real number increments, and six additional real number arithmetic operations. Simpson’s rule involves (n + 2) function evaluations, n real number increments, and ten additional real number arithmetic operations. Gauss-Legendre quadrature uses n function evaluations, 3 * n real number arithmetic operations, 2 * n index operations, and five additional arithmetic operations. Finally, the Monte Carlo Method requires n function evaluations, n random number generations, 2 * n + 3 additional real number arithmetic operations. The Gauss-Legendre quadrature also involves some complicated orthogonal polynomial operations to determine the abscissas and weights. Below are some results from our test C# application.

ResultsForm 10_25_2018 5_20_34 PM ResultsForm 10_25_2018 5_21_14 PM ResultsForm 10_25_2018 5_21_28 PM ResultsForm 10_25_2018 5_22_26 PM ResultsForm 10_25_2018 5_22_47 PM ResultsForm 10_25_2018 5_23_05 PM ResultsForm 10_25_2018 5_23_52 PM ResultsForm 10_25_2018 5_24_19 PM ResultsForm 10_25_2018 5_24_39 PM

We conclude from the preceding dearth of tests that for given n the order of accuracy is generally Gauss-Legendre, Simpson’s, Trapezoidal, and finally Monte Carlo.

ASP .NET AJAX Timer Demonstration by James Pate Williams, Jr. BA, BS, MSwE, PhD

Sometimes in a web application you want to time the user’s input. Suppose you have a one textbox web form and you want to set an inactivity timer of 1200 seconds which is equal to 20 minutes. Every time the user adds or modifies the textbox the timer is reset to 0. The following pictures tell the story of my implementation of such a server-side timer in ASP .NET using an AJAX timer object.

Microsoft Edge 10_13_2018 4_29_27 PM Microsoft Edge 10_13_2018 4_30_22 PM Microsoft Edge 10_13_2018 4_31_27 PM Microsoft Edge 10_13_2018 4_51_20 PM Microsoft Edge 10_13_2018 4_52_03 PM Microsoft Edge 10_13_2018 4_57_43 PM

AJAX Timer Demonstration Source Code

Calculating a Few Digits of the Transcendental Number Pi by Throwing Darts by James Pate Williams, BA, BS, MSwE, PhD

Suppose you have a unit square with a circle of unit diameter inscribed . You can compute a few digits of the transcendental number, pi, 3.1415926535897932384626433832795…, by using the algorithm described as follows. Let n be the number of darts to throw and h be the number of darts that land within the inscribed circle.

h = 0

for i = 1 to n do

Choose two random numbers x and y such that x and y are contained in the interval 0 to 1 inclusive that is x and y contained in [0, 1]

Let u = x – 1 / 2 and v = y – 1 / 2

if u * u + v * v <= 0.25 = 1 / 4 then h = h + 1

next i

pi = 4 * h / n

Below are the results of a C# Microsoft Visual Studio simulation project. In the first case we throw 100,000 darts and get two significant digits of pi and then we throw a 1,000,000 darts and five significant digits of pi are computed. Of course, in a previous entry by this author we can calculate hundreds or thousands of digits of pi in relatively little time:

https://jamespatewilliamsjr.wordpress.com/2018/07/01/the-bailey-borwein-plouffe-formula-for-calculating-the-first-n-digits-of-pi/

MainForm 10_16_2018 3_04_04 AM MainForm 10_16_2018 3_05_45 AM MainForm 10_16_2018 3_09_36 AM MainForm 10_16_2018 3_09_54 AM