Category: Elementary Physics
A Matrix Identity

Some Elementary Quantum Mechaincs (c) Thursday, May 16, 2024, by James Pate Williams, Jr.
Text and Exercise from “Boundary Value Problems Second Edition” by David L. Powers in Progress (c) Wednesday, April 17, 2024, James Pate Williams, Jr.
Solution of the Laplace (Potential) Equation on a Two-Dimensional Square via Finite Differences
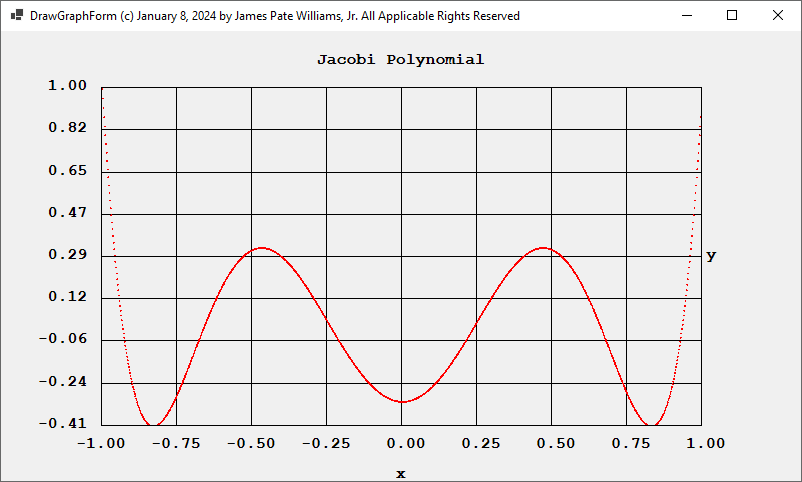
New Jacobi Polynomials Application January 8, 2024, by James Pate Williams, Jr.
The two primary references used to create my application were: “A Numerical Library in C for Scientists and Engineers” by H. T. Lau and the following website: https://en.wikipedia.org/wiki/Jacobi_polynomials.
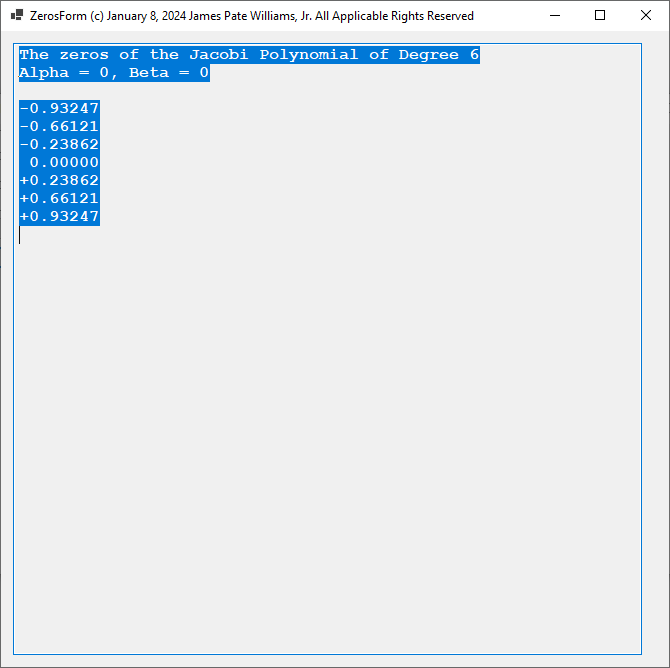
Using the Jacobi parameters alpha = 0 and beta = 0, we have the Legendre polynomials for degrees 4 and 6 and their associated roots:


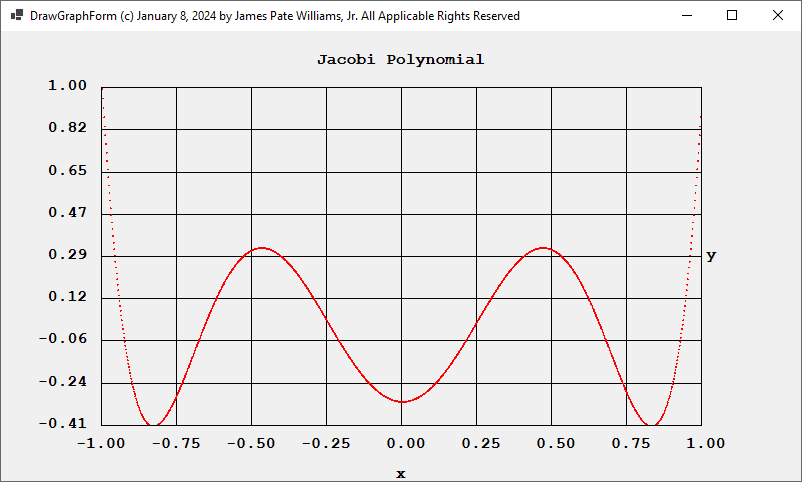
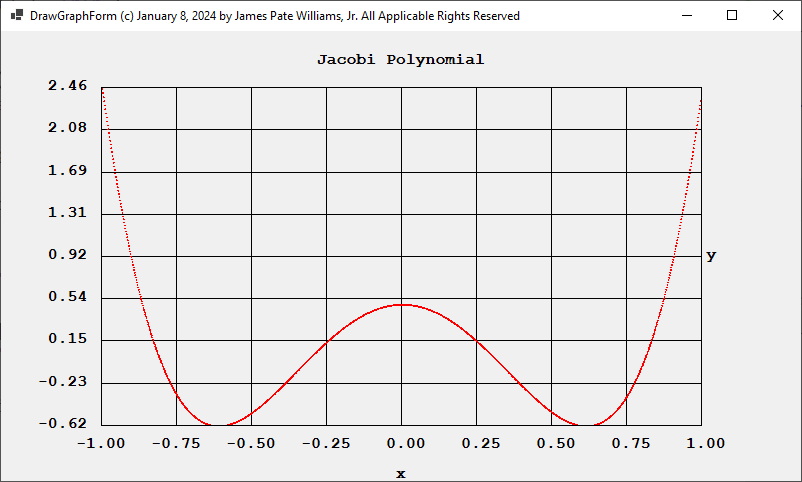
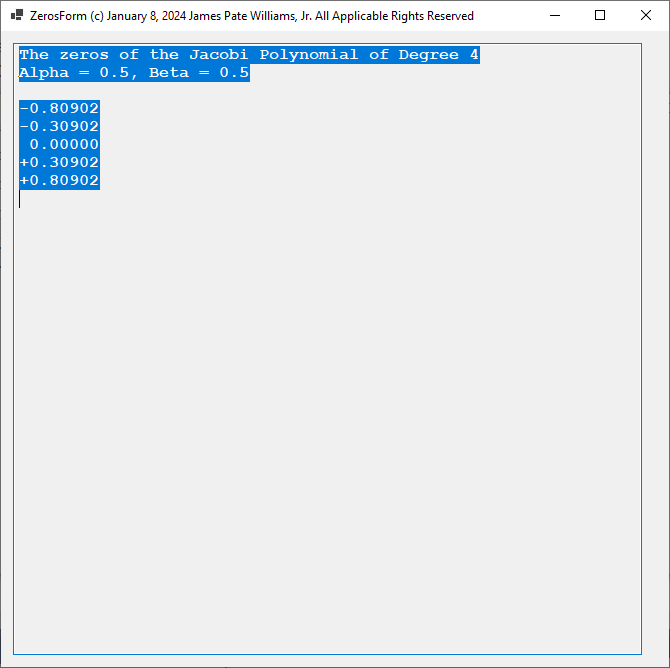
Using alpha = 0.5 and beta= 0.5 we obtain for degrees 4 and 6:

Electron Probability Distribution Function Etc. (c) James Pate Williams, Jr. December 2023
More than Four Dimensions Why Worry a Blog Entry by James Pate Williams, Jr. December 27, 2023
Some modern physical models of our universe require more than Einstein’s four dimensions: three spatial dimensions and one time dimension. Why do people worry about introducing more dimensions into our understanding of chemistry and physics? When Erwin Schrödinger introduced his famous quantum mechanical two-body solution of the time independent hydrogen-like atom wave equation he went four dimensions to three spatial dimensions. Later, Wolfgang Pauli espoused his famous Pauli Exclusion Principle that simply stated no two electrons (fermions) in an atomic orbital can have the same quantum spin number. Atoms live in a four-dimensional quantum number space augmented by three spatial dimensions and one time dimension.