Tag: Numerical Analysis

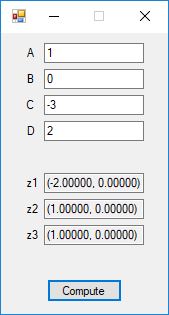
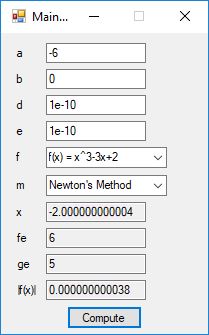
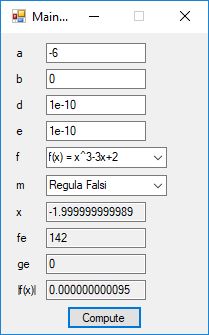
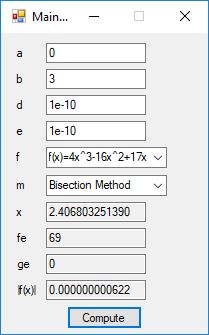
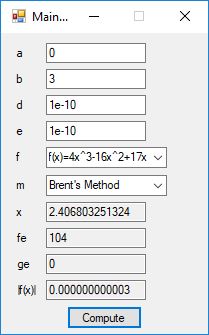
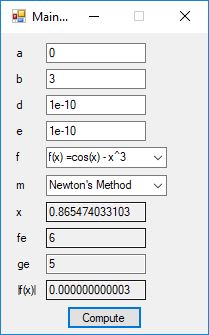
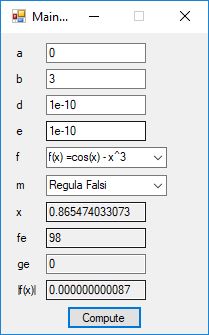
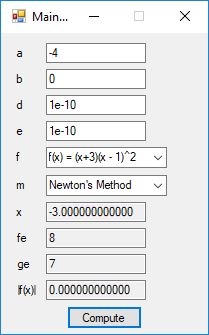
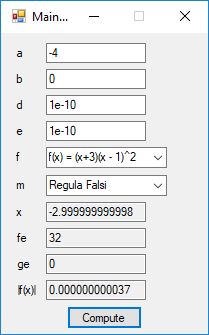
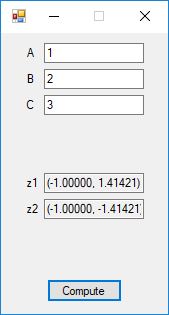
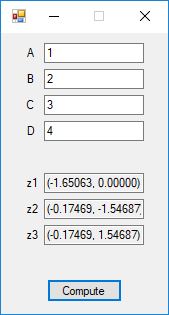
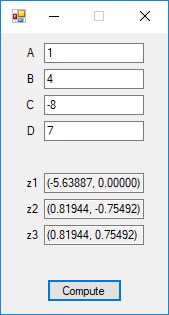
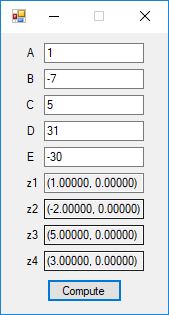
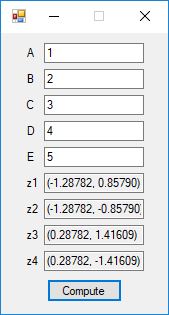
The Bailey-Borwein-Plouffe formula for determining the digits of pi was discovered in 1995. This formula has been utilized to find the exact digits of pi to many decimal places.

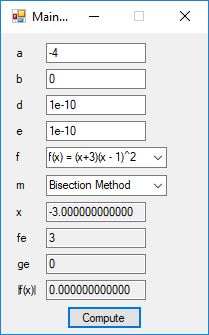
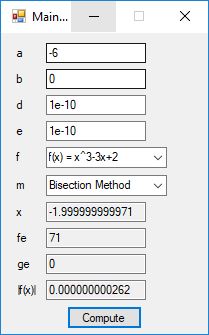
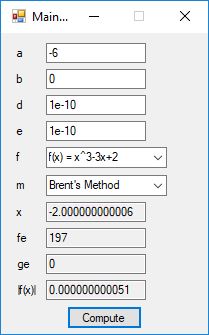
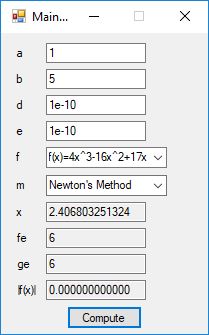
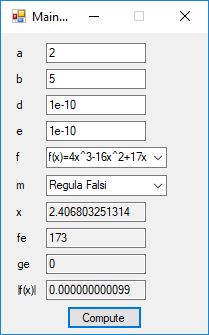
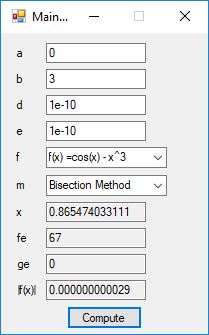
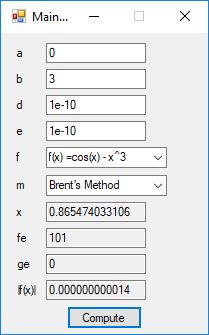
I recently re-implemented my legacy C and FreeLIP program that utilized the BBP formula. The new C# application uses a homegrown big unsigned decimal number package that includes methods for +, -, *, / operators and an exponentiation (power) function. I used short integers (16-bit signed integers) to represent the individual digits of the number in any base whose square can be expressed as a positive short integer. That includes the decimal base 10 and hexadecimal base 16. For this application the base was chosen to be 10. Also, included was a n-digits of pi function that used the C# language’s built-in BigInteger data type.  Below are some screen shots of the program in action.

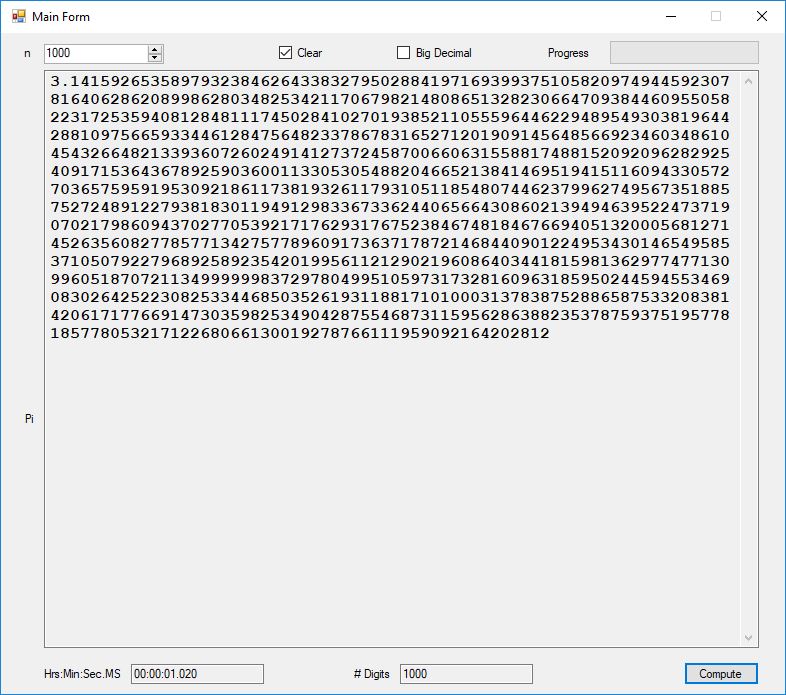
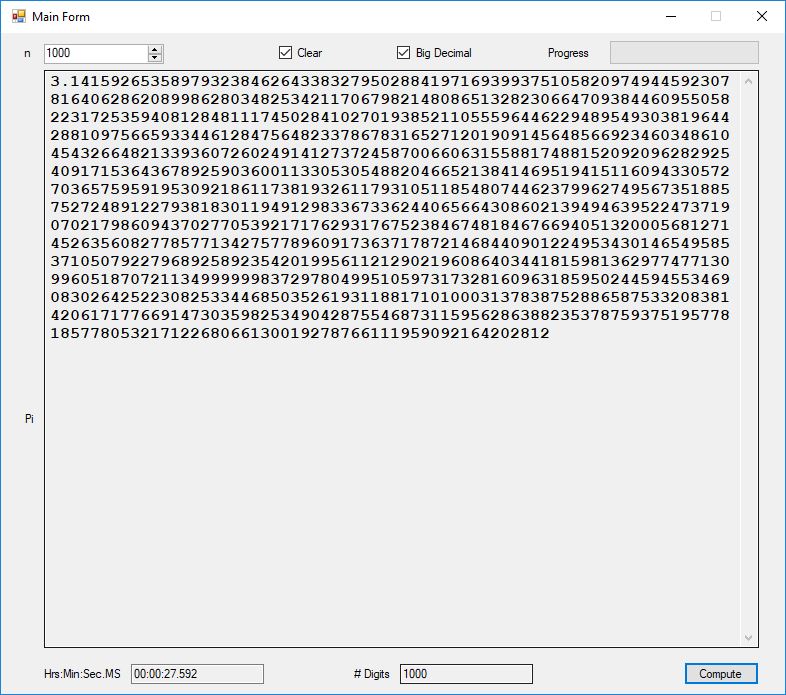
As you can easily see the BigInteger implementation is an order of magnitude faster that the BigDecimal version (actually around 27+ times faster).

Last, we include a link to a PDF containing data comparing calculations performed on a Intel based desktop versus an AMD based laptop.

Benchmark Calculations Using the Application BigIntegerPi