I designed and implemented a C# computer language application to model the temperature anomaly data found on the NOAA website:
I used the latest recommended data for time period 1895 to 2017. The empirical modeling paradigm I used was simple linear regression. My model goes out to the year 2300. The key formulas used by the model are:
See the website:
https://en.wikipedia.org/wiki/Simple_linear_regression
Below are some plots of the temperature anomaly.
Solve the Laplace equation in the following orthogonal rectilinear coordinate systems:
Solution PDF:
The four methods considered in this study are as follows:
The trapezoidal rule requires (n + 2) function evaluations, n real number increments, and six additional real number arithmetic operations. Simpson’s rule involves (n + 2) function evaluations, n real number increments, and ten additional real number arithmetic operations. Gauss-Legendre quadrature uses n function evaluations, 3 * n real number arithmetic operations, 2 * n index operations, and five additional arithmetic operations. Finally, the Monte Carlo Method requires n function evaluations, n random number generations, 2 * n + 3 additional real number arithmetic operations. The Gauss-Legendre quadrature also involves some complicated orthogonal polynomial operations to determine the abscissas and weights. Below are some results from our test C# application.
We conclude from the preceding dearth of tests that for given n the order of accuracy is generally Gauss-Legendre, Simpson’s, Trapezoidal, and finally Monte Carlo.
Sometimes in a web application you want to time the user’s input. Suppose you have a one textbox web form and you want to set an inactivity timer of 1200 seconds which is equal to 20 minutes. Every time the user adds or modifies the textbox the timer is reset to 0. The following pictures tell the story of my implementation of such a server-side timer in ASP .NET using an AJAX timer object.
Suppose you have a unit square with a circle of unit diameter inscribed . You can compute a few digits of the transcendental number, pi, 3.1415926535897932384626433832795…, by using the algorithm described as follows. Let n be the number of darts to throw and h be the number of darts that land within the inscribed circle.
h = 0
for i = 1 to n do
Choose two random numbers x and y such that x and y are contained in the interval 0 to 1 inclusive that is x and y contained in [0, 1]
Let u = x – 1 / 2 and v = y – 1 / 2
if u * u + v * v <= 0.25 = 1 / 4 then h = h + 1
next i
pi = 4 * h / n
Below are the results of a C# Microsoft Visual Studio simulation project. In the first case we throw 100,000 darts and get two significant digits of pi and then we throw a 1,000,000 darts and five significant digits of pi are computed. Of course, in a previous entry by this author we can calculate hundreds or thousands of digits of pi in relatively little time:
We designed and implemented a C# application that uses the following root finding algorithms:
https://en.wikipedia.org/wiki/Bisection_method
https://en.wikipedia.org/wiki/Brent%27s_method
https://en.wikipedia.org/wiki/Newton%27s_method
https://en.wikipedia.org/wiki/False_position_method
The source code files are displayed below as Word files:
We designed and implemented quadratic formula, cubic formula, and quartic formula solvers using the formulas in the Wikipedia articles:
https://en.wikipedia.org/wiki/Quadratic_formula
https://en.wikipedia.org/wiki/Cubic_function
https://en.wikipedia.org/wiki/Quartic_function
We tested our C# implementation against:
https://keisan.casio.com/exec/system/1181809415
http://www.wolframalpha.com/widgets/view.jsp?id=3f4366aeb9c157cf9a30c90693eafc55
https://keisan.casio.com/exec/system/1181809416
Here are screenshots of the C# application:
C# source code files for the application:
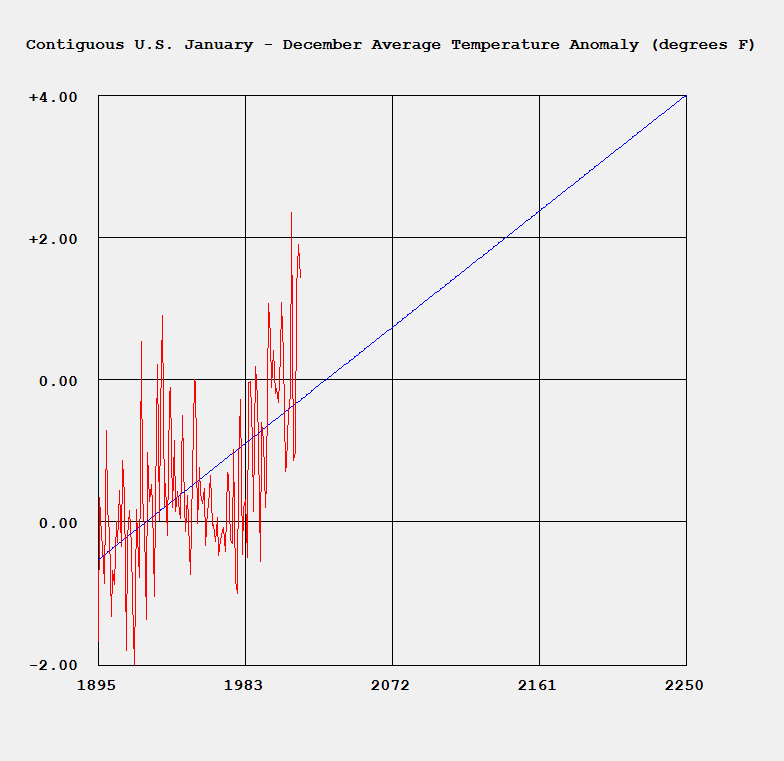
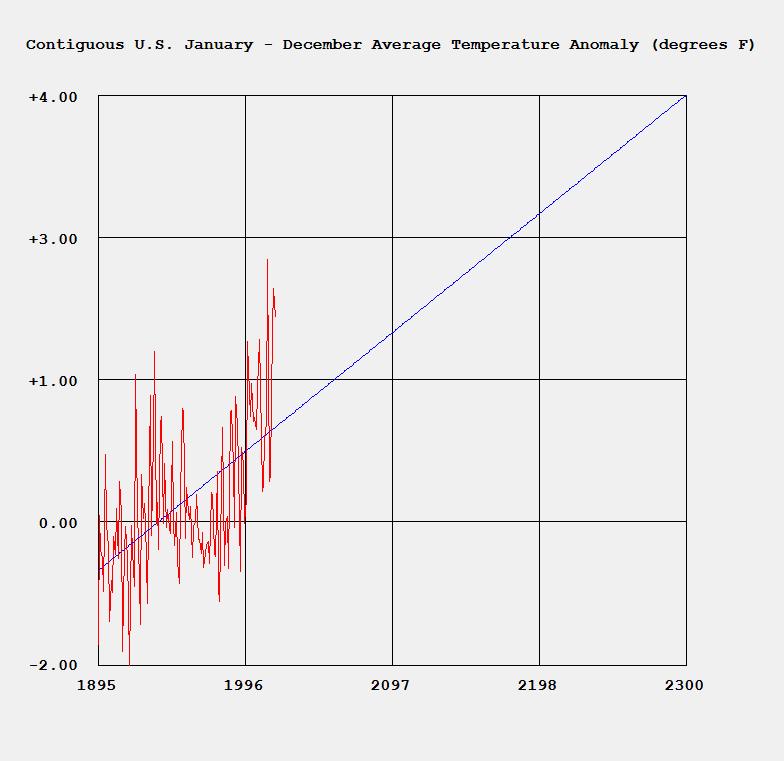
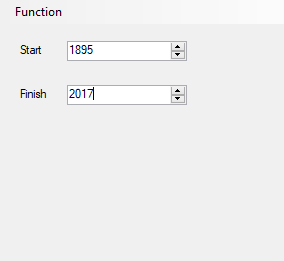
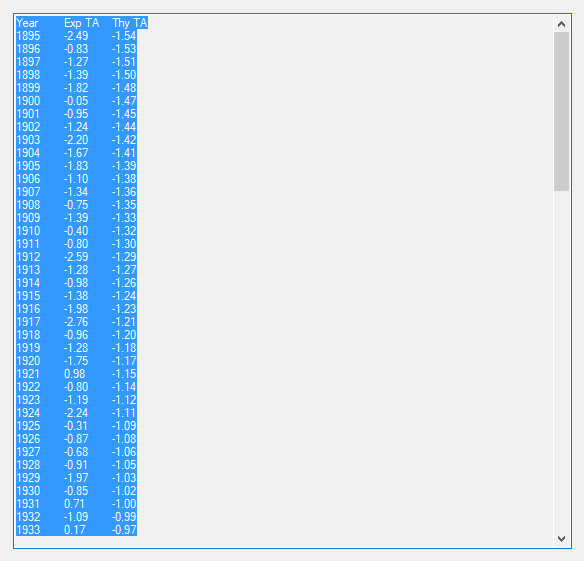
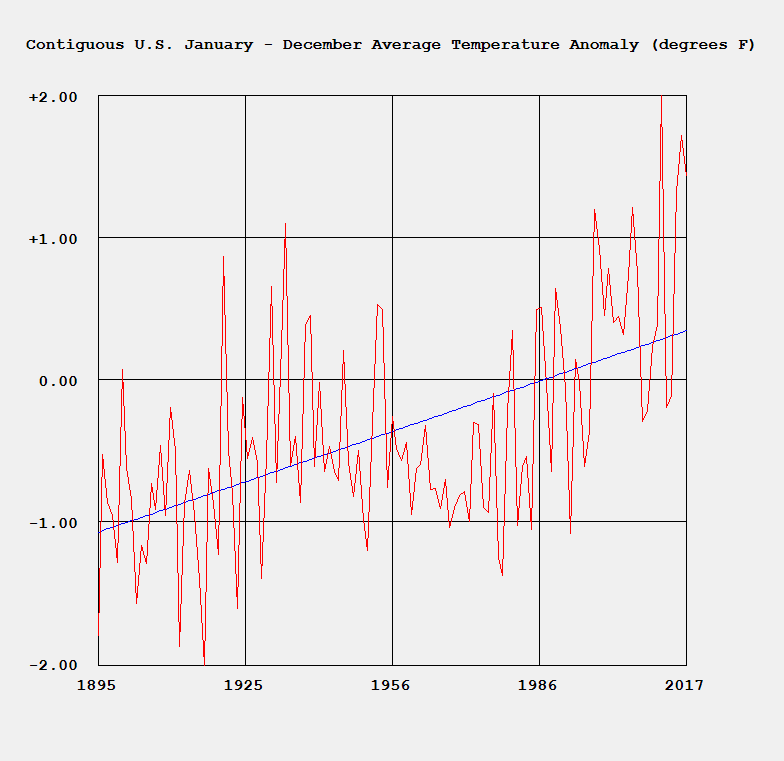
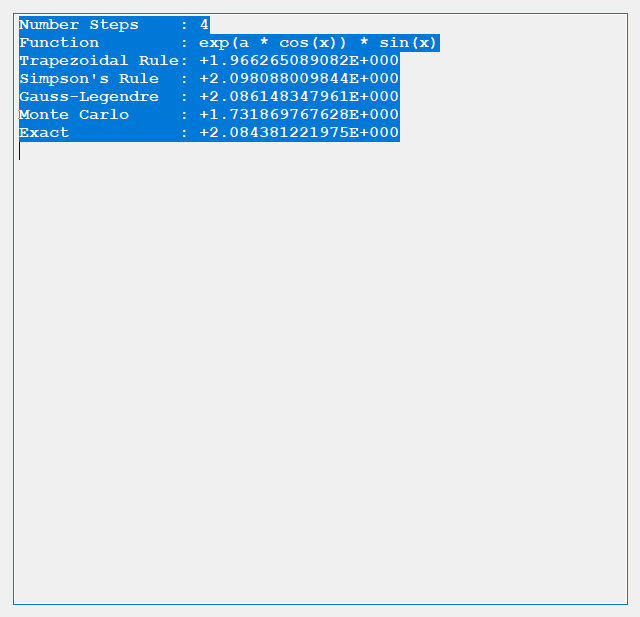
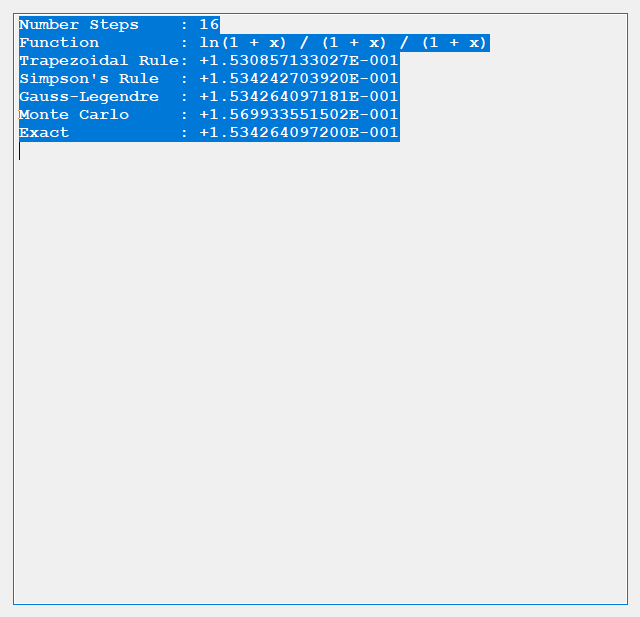
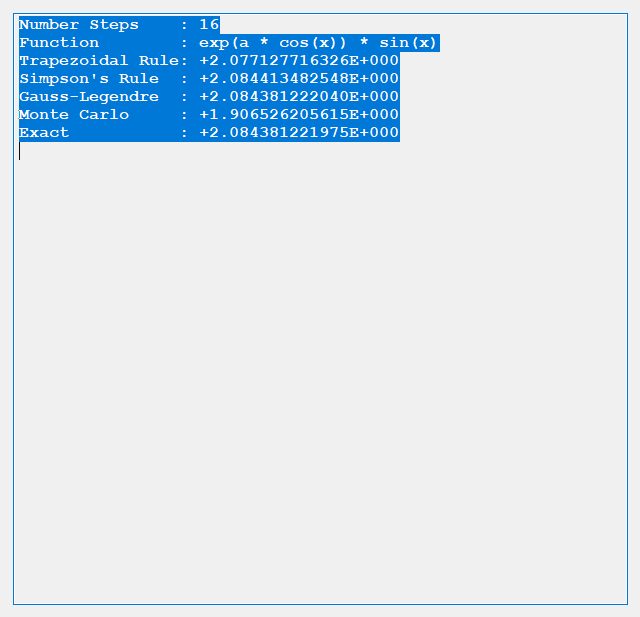
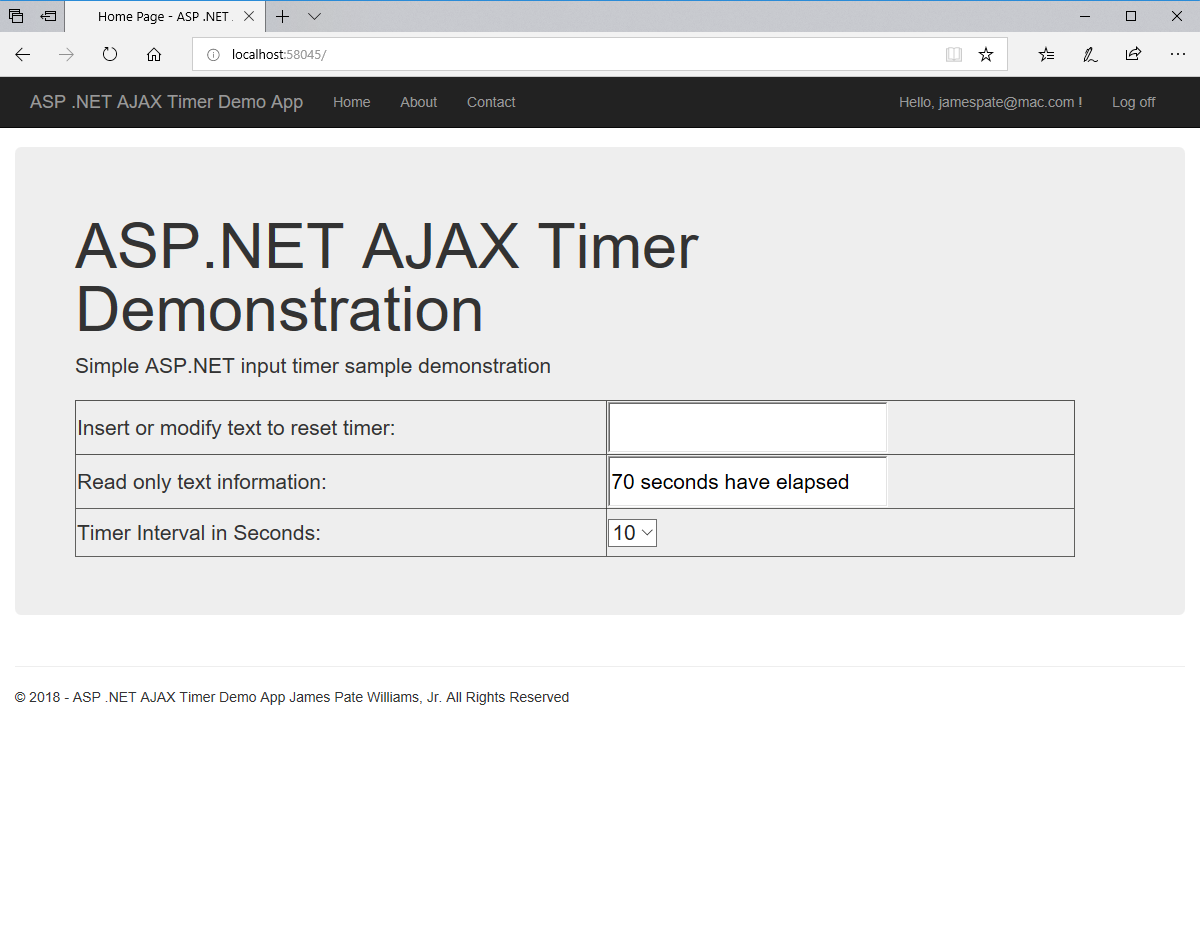
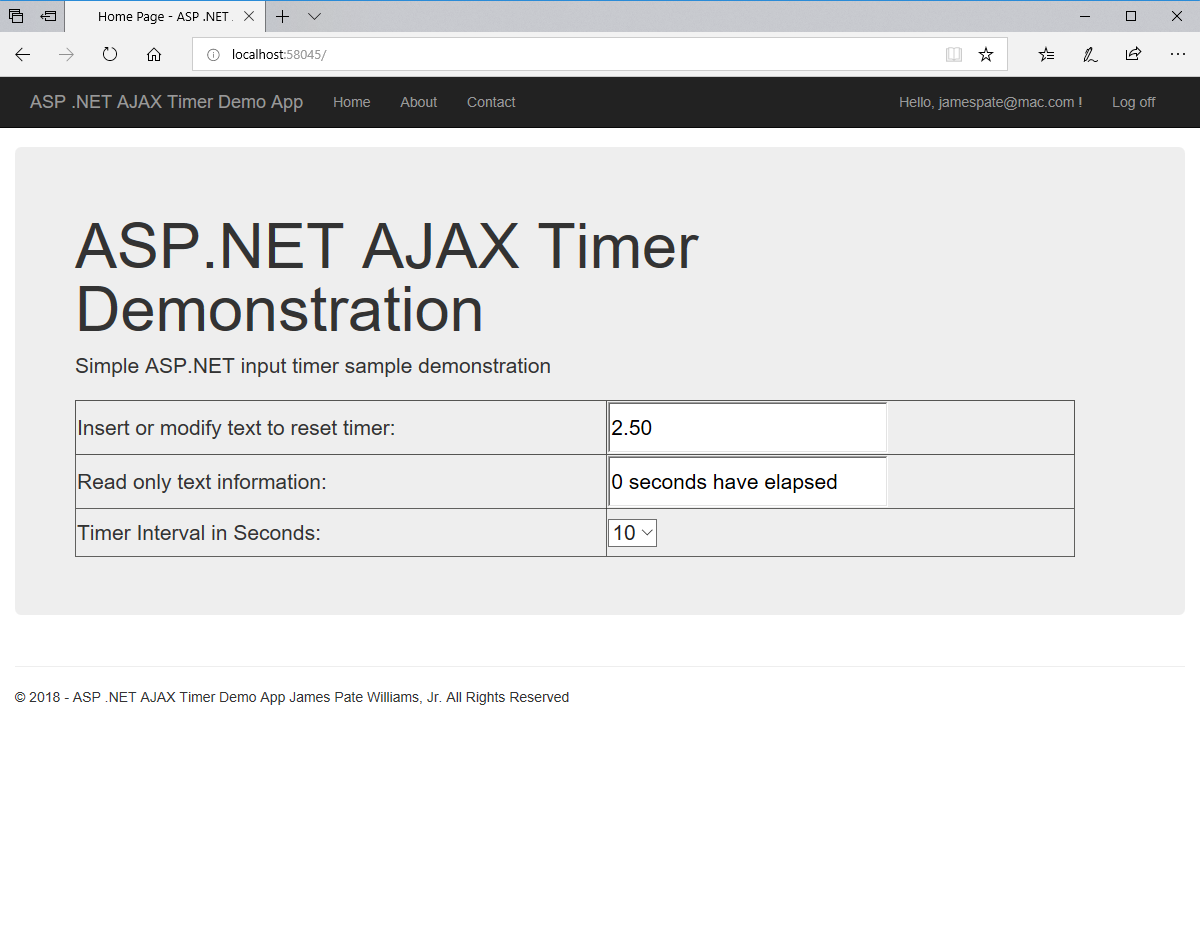
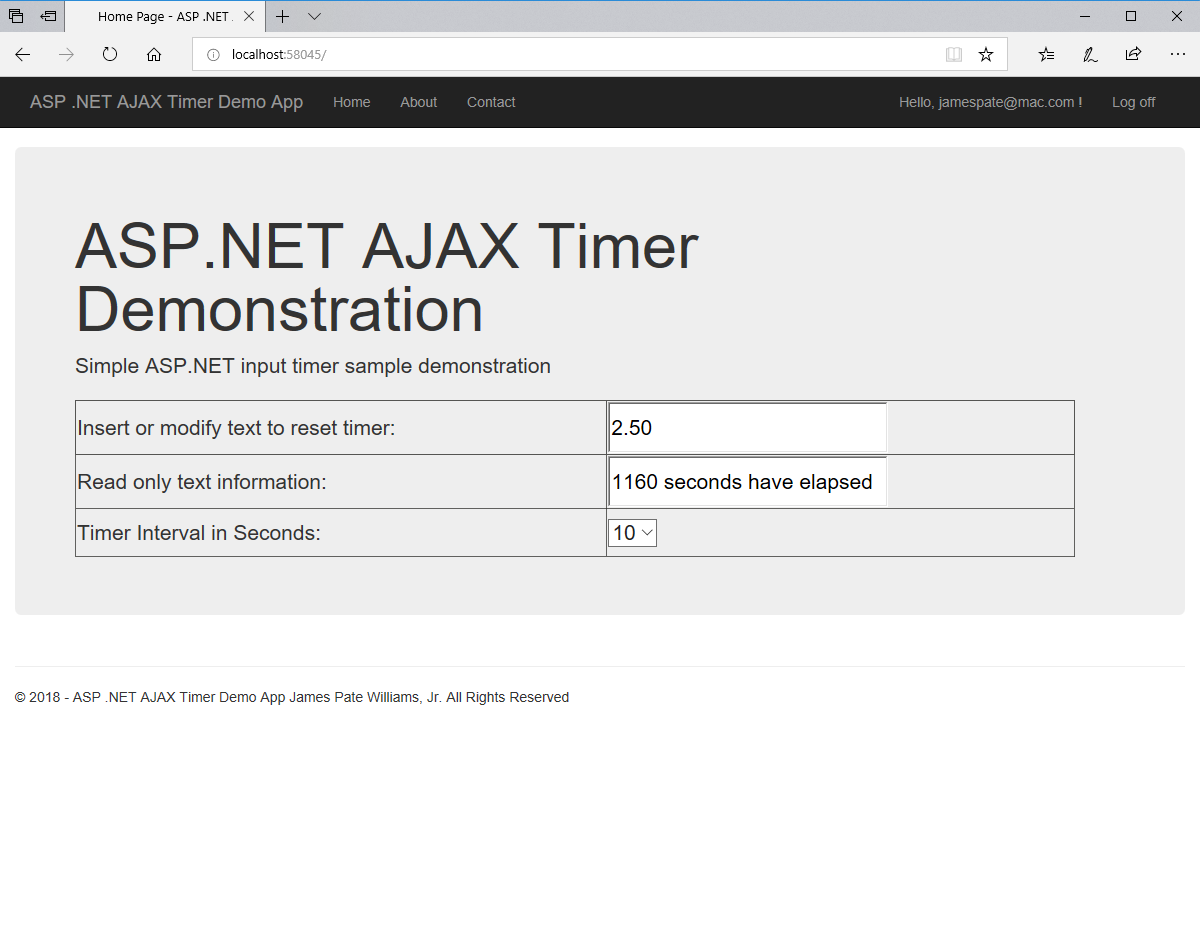
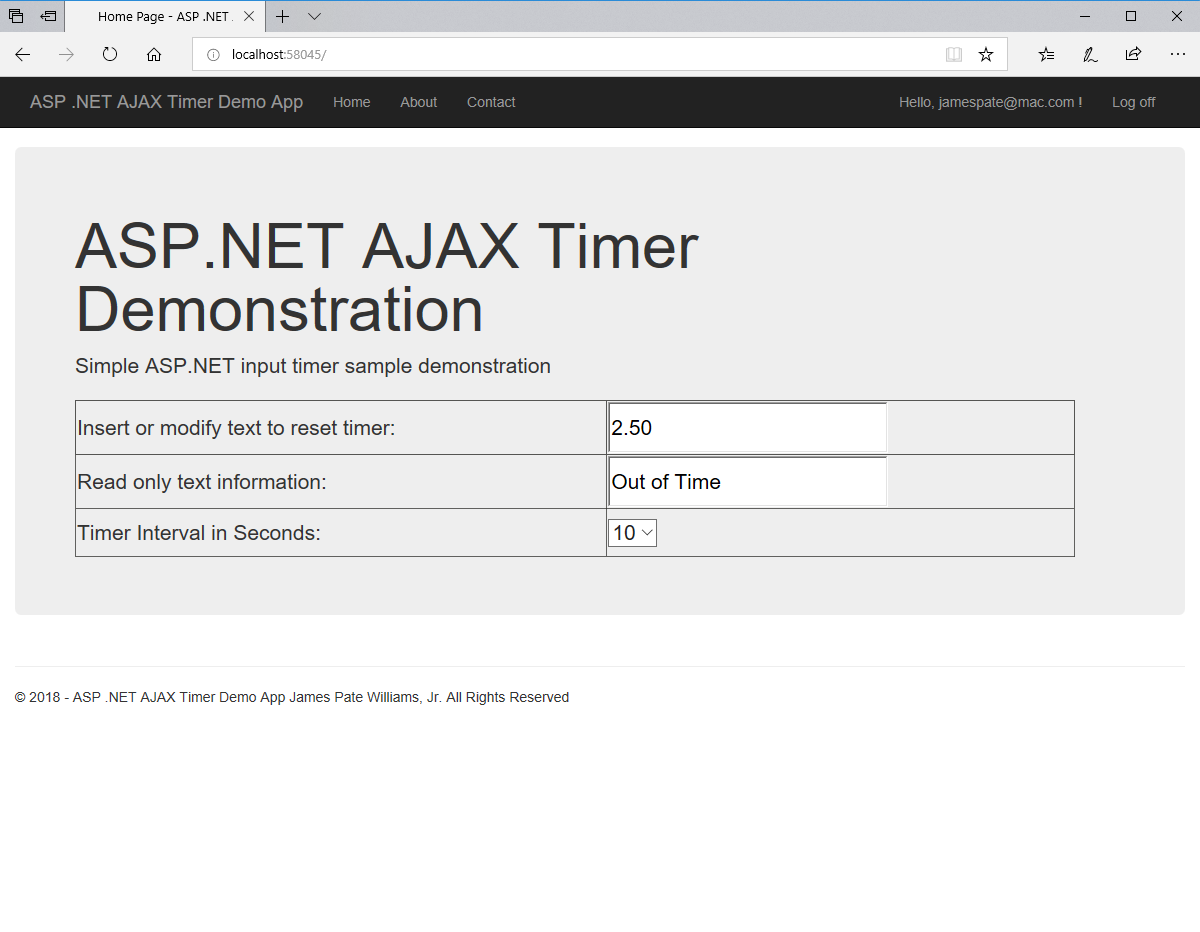
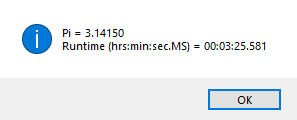
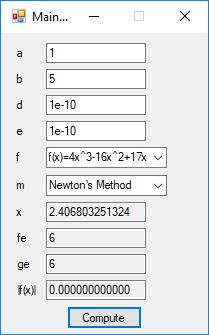
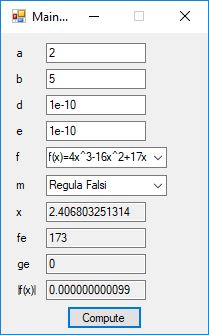
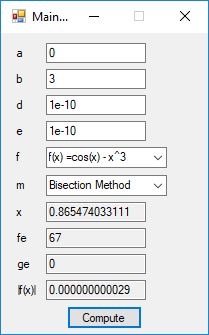
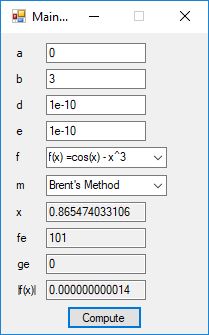
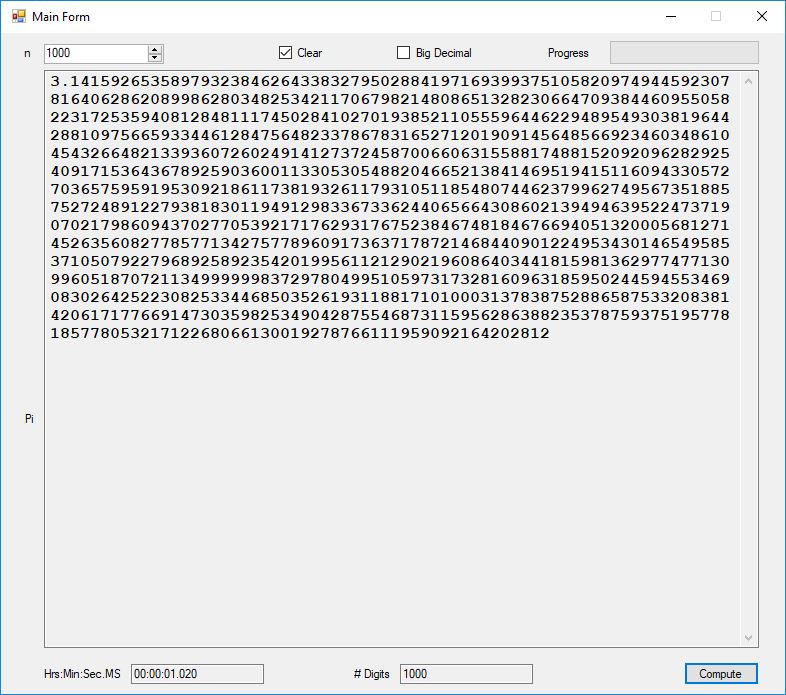
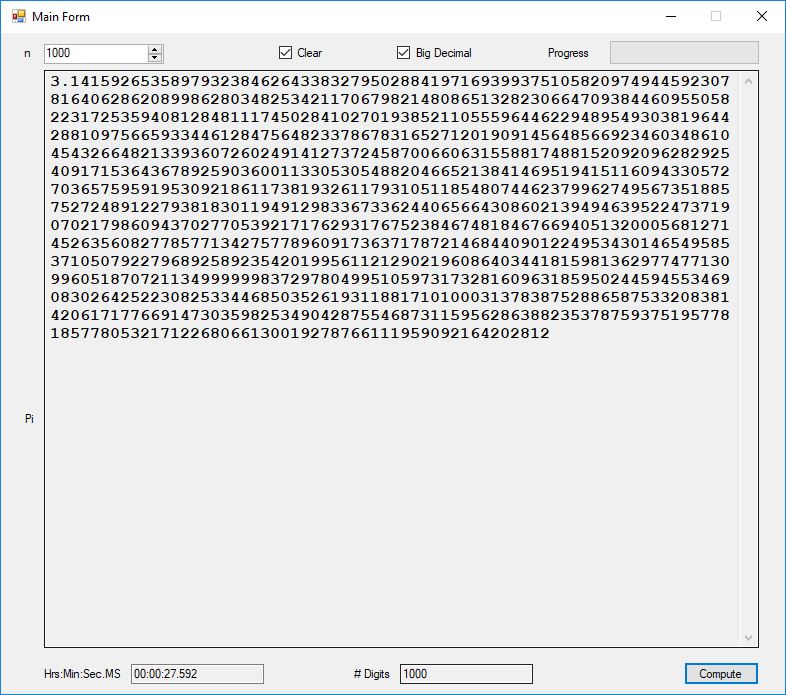
We designed and implemented a simple and utilitarian C# matrix class for double precision numbers. The class has the binary matrix operators +, -, *, / which are addition, subtraction, multiplication, and division of two matrices. We also include an operator for multiplication of matrix by a scalar and an operator for dividing a matrix by a scalar. We have included functions to compute the p-norm, p, q-norm, and max norm of a matrix. We also can calculate using truncated infinite series the exponential, cosine, and sine function of a matrix. The exponential and trigonometric functions use a powering function that raises a matrix to a non-negative integral power.
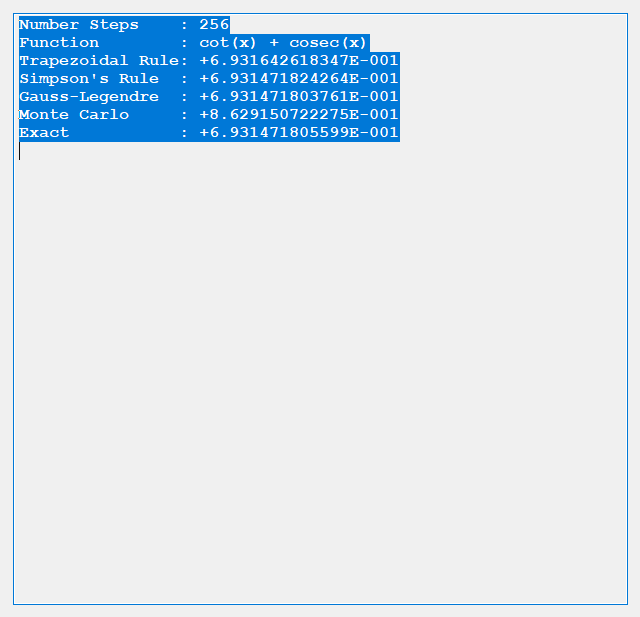
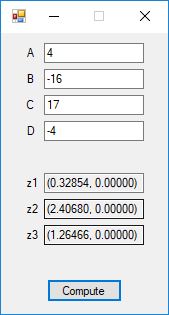
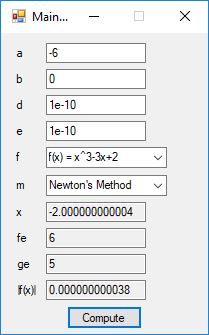
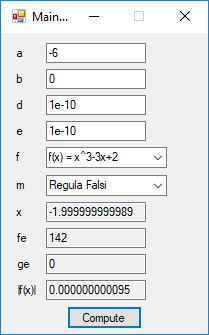
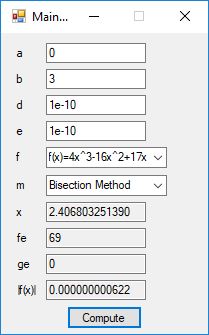
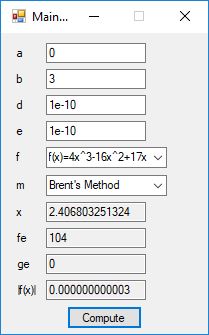
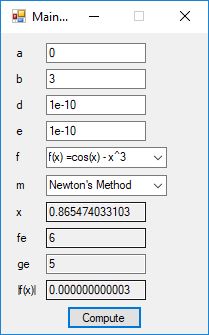
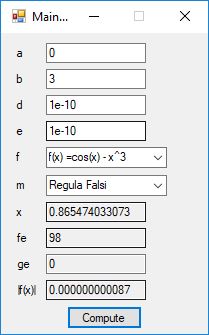
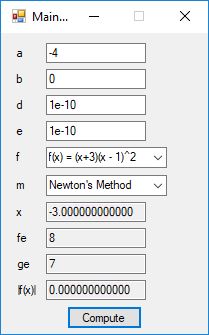
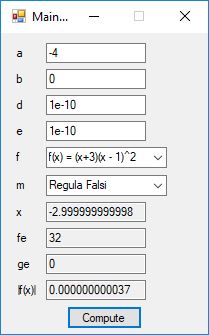
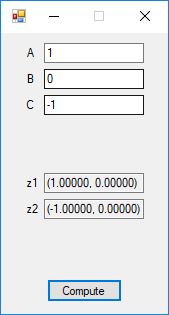
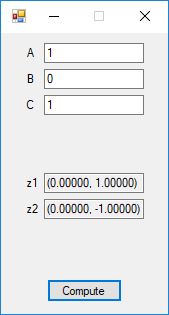
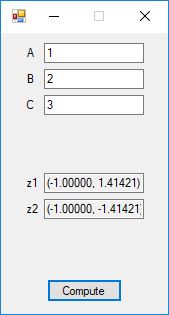
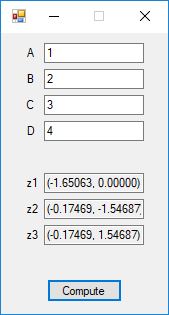
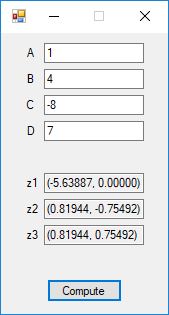
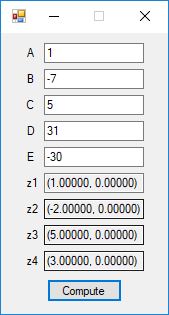
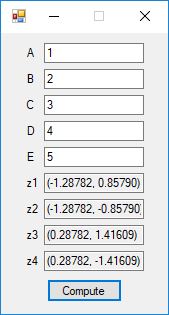
Below is a screenshot of the test Windows Forms application. We execute the four binary matrix operators in the order +, -, *, / e.g. A+B, A-B, A*B, A/B. In order to divide by B, the matrix B must be square and non-singular, that is square and invertible.
The B matrix has the form of the matrix in the online discussion:
http://www.purplemath.com/modules/mtrxinvr2.htm
We create a project named MatrixExample. In this project we add a Matrix class whose code is given below:
I leave it as an exercise for the reader to test the various norms and other functions.
The Bailey-Borwein-Plouffe formula for determining the digits of pi was discovered in 1995. This formula has been utilized to find the exact digits of pi to many decimal places.
I recently re-implemented my legacy C and FreeLIP program that utilized the BBP formula. The new C# application uses a homegrown big unsigned decimal number package that includes methods for +, -, *, / operators and an exponentiation (power) function. I used short integers (16-bit signed integers) to represent the individual digits of the number in any base whose square can be expressed as a positive short integer. That includes the decimal base 10 and hexadecimal base 16. For this application the base was chosen to be 10. Also, included was a n-digits of pi function that used the C# language’s built-in BigInteger data type. Below are some screen shots of the program in action.
As you can easily see the BigInteger implementation is an order of magnitude faster that the BigDecimal version (actually around 27+ times faster).
Last, we include a link to a PDF containing data comparing calculations performed on a Intel based desktop versus an AMD based laptop.
After successfully downloading and installing a free one-month trial evaluation version of Microsoft’s Visual Studio 2017 Professional Graphical User Interface Integrated Development Environment, I decided to try my hand at creating an Office VSTO Add-In. I chose the computer language C# and the Office application Outlook. Among other functions Outlook is a personal computer’s email client for IMAP or POP3. The problem that the add-in solves is a preliminary evaluation of the meaning of an email’s body. The add-in counts the frequency of occurrence of the following (assuming English language):
Once an email is opened and in an active inspector the OutlookAddIn1’s Outlook ribbon is displayed with 12 edit boxes that contain the counts enumerated in the preceding numbered list. Below is an email that illustrates night of the frequency tabulations.
The next email contains danger, cuss, and hate words.
https://social.technet.microsoft.com/Profile/james%20pate%20williams%20jr
https://www.facebook.com/pg/JamesPateWilliamsJrConsultant/posts/
Numerical Explorations 