Computer Science – Page 4 – Numerical Explorations

Five Stream Ciphers Created from Five Pseudorandom Number Generators Built Using the Tests of FIPS 140-1 by James Pate Williams, BA, BS, MSwE, PhD

The five pseudorandom number generators are:

Triple-AES based ANSI X9.17 PRNG
Triple-DES based ANSI x9.17 PRNG
RSA based PRNG
Micali-Schnorr PRNG
Blum-Blum-Shub PRNG

Five stream ciphers were created using 1 to 5. Screenshots of the C# application follow:

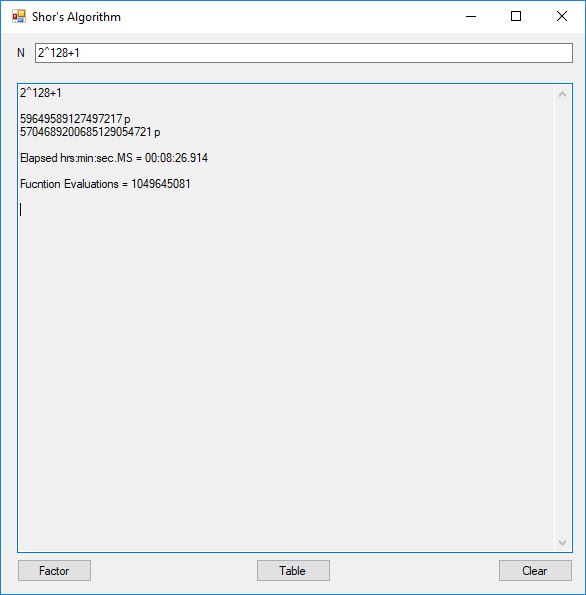
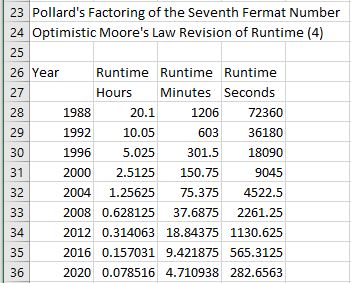
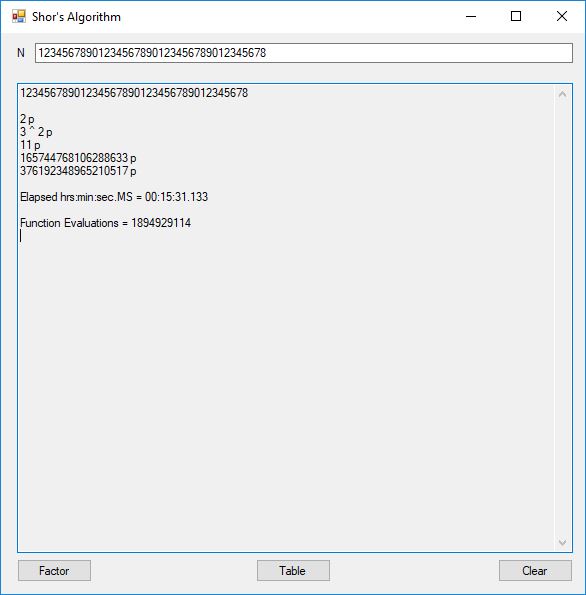
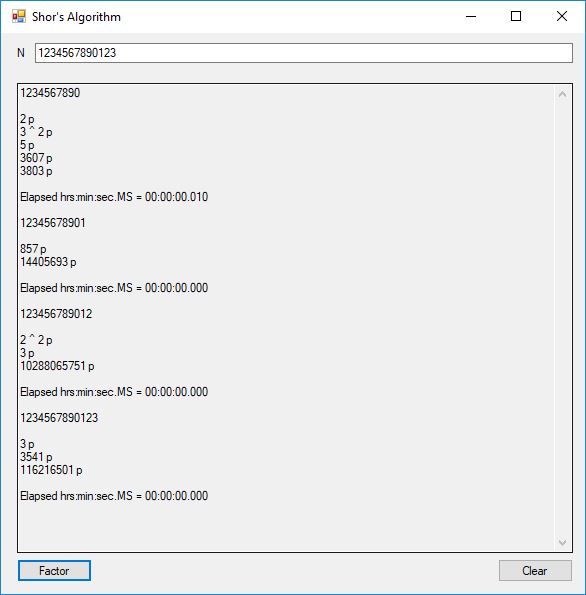
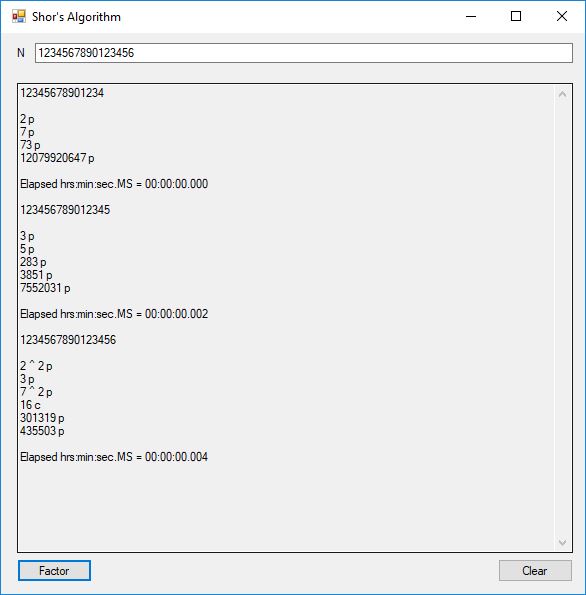
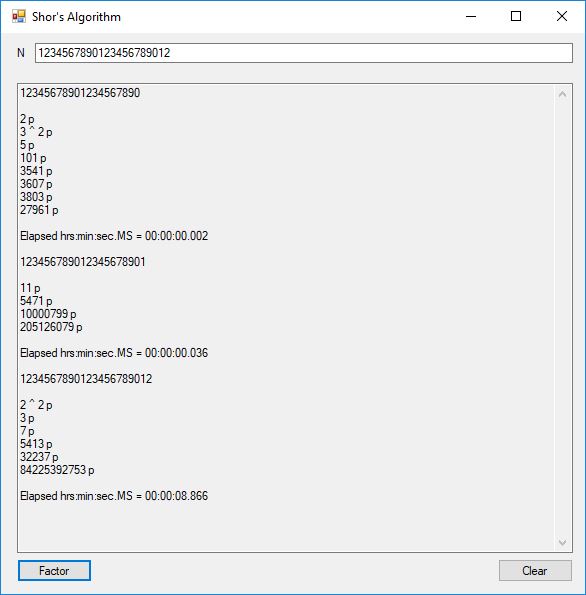
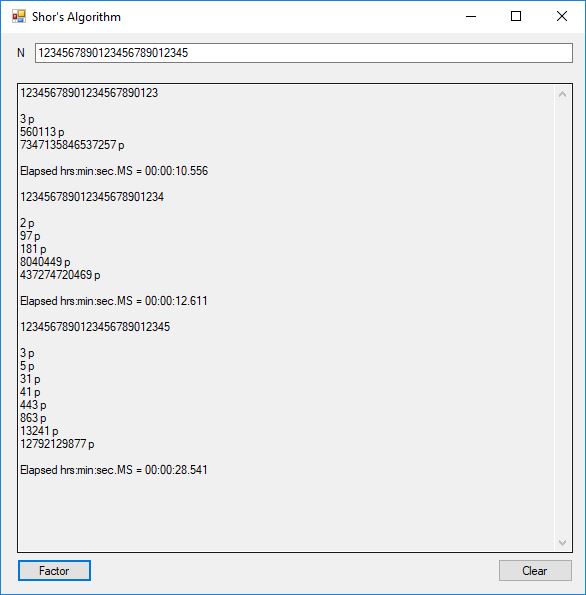
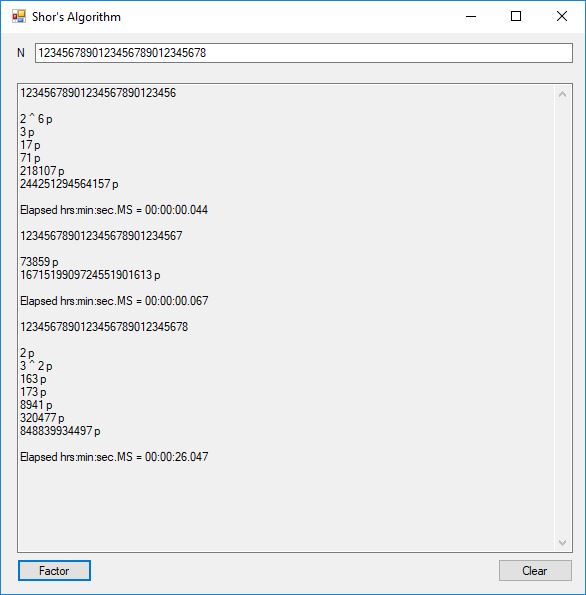
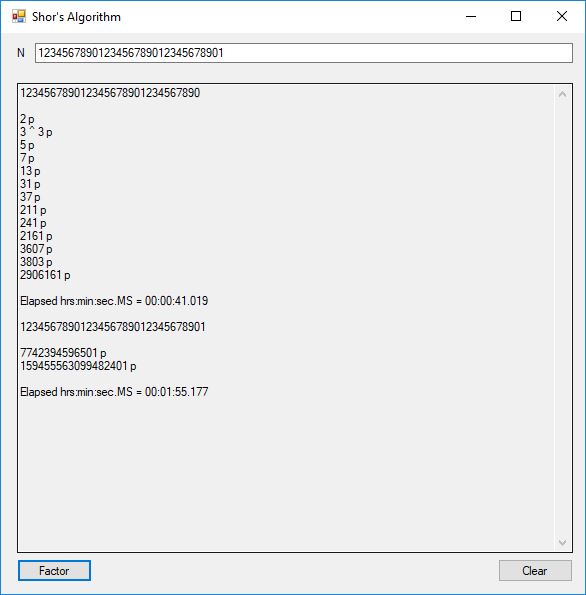
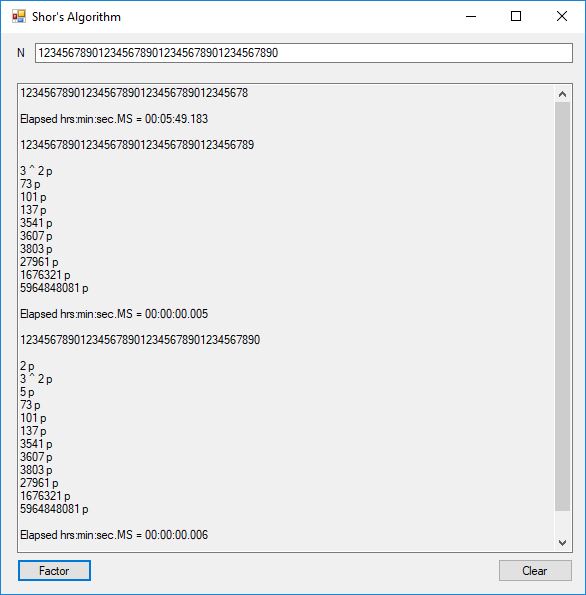
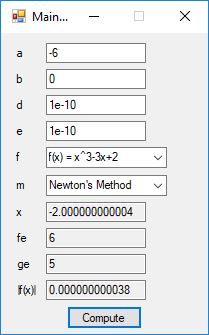
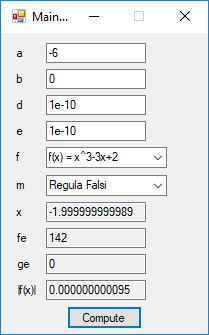
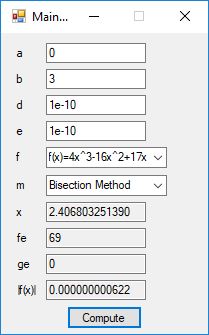
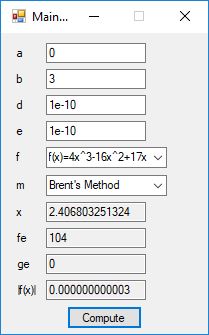
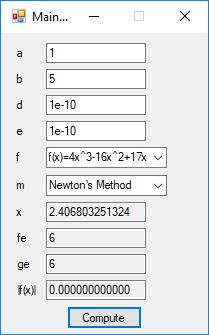
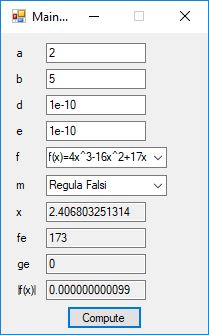
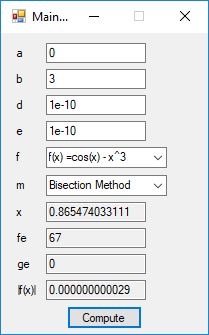
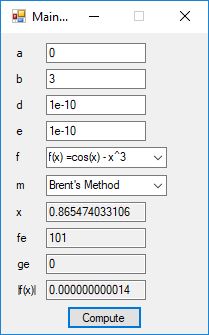
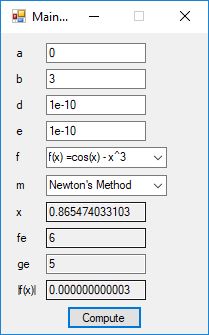
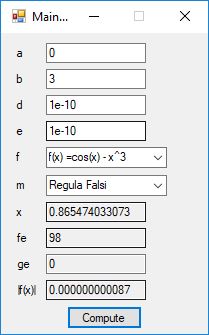
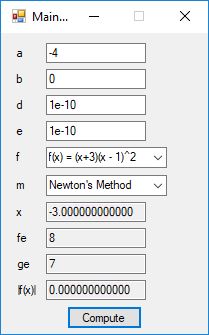
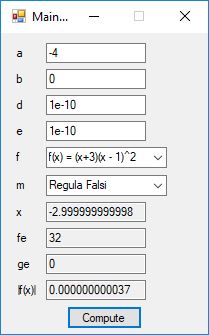
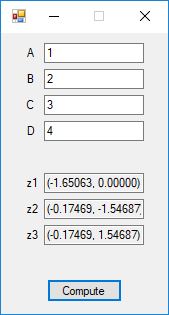
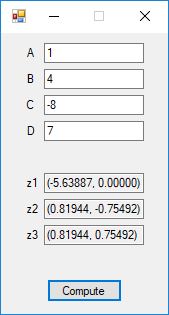
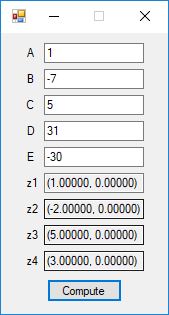
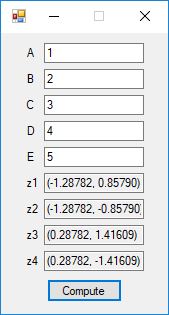
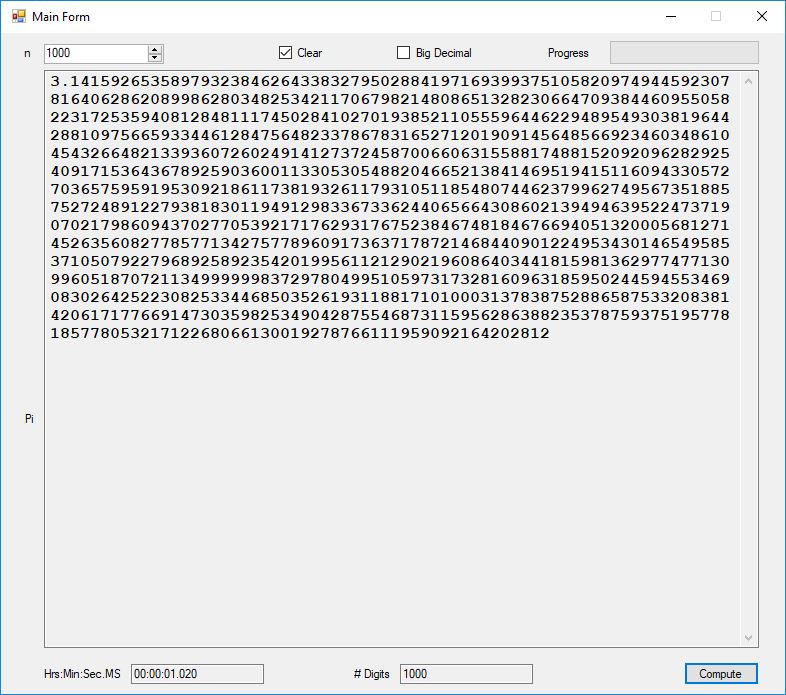
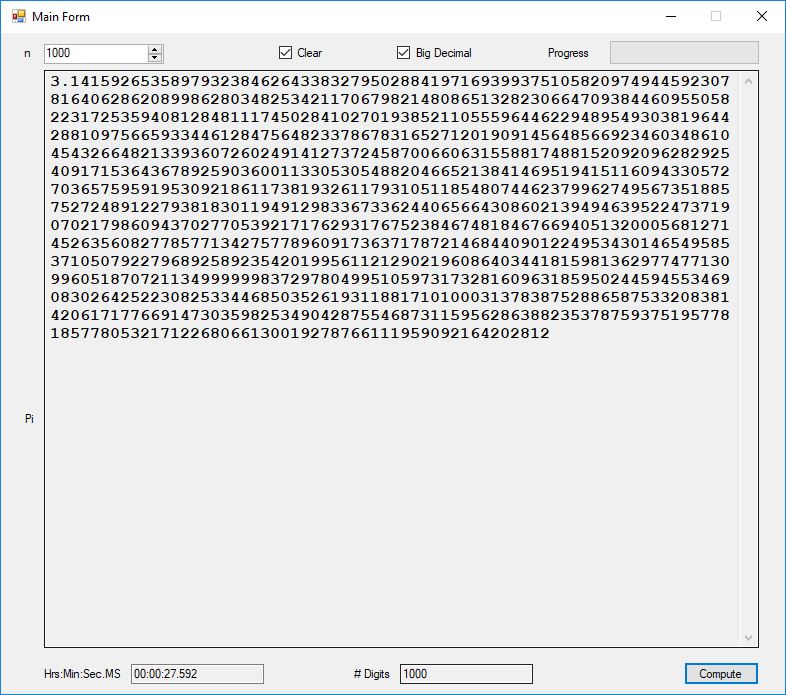
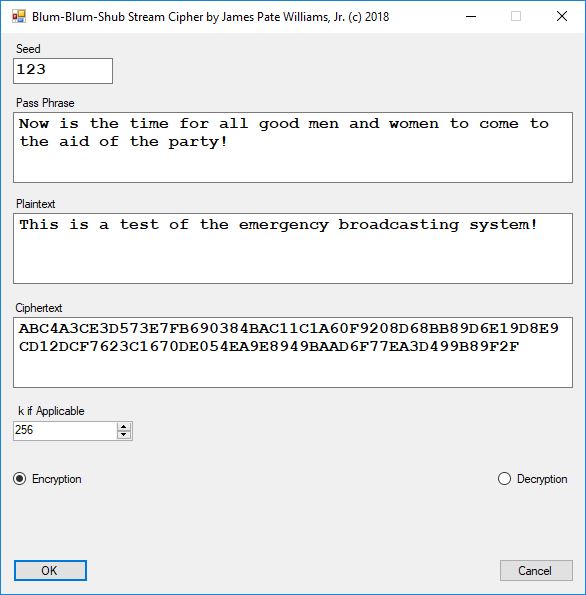
sc aes sc des sc rsa sc ms sc bbs

The pass phrase optimally should consist of 147 ASCII characters. If the number of pass phrase ASCII characters is less than 147 then more random ASCII characters are added using the standard C# pseudorandom number generator seeded with the parameter named Seed. The user defined parameter k is used by RSA, Micali-Schnorr, and Blum-Blum-Shub pseudorandom number generators. It is the approximate bit length of the large composite number composed of two large probable prime numbers. The real key lengths of all the stream ciphers is about 1024-bits for 1, 3, 4, and 5 and 296-bits for 2. I’d strongly suggest using 1 and/or 5.

Tests of Six Pseudorandom Number Generators (PRNGs) Using the Now Superseded FIPS 140-1 by James Pate Williams, Jr. BA, BS, MSwE, PhD

This blog explores six pseudorandom number generators which are enumerated as follows:

Standard C# PRNG
Triple-AES PRNG
Triple-DES PRNG
RSA Based PRNG
Micali-Schnorr PRNG
Blum-Blum-Shub PRNG

PT 00 PT 01 PT 02 PT 03 PT 04 PT 05

Here is the order in terms of run-times from the fastest to the slowest: 1, 2, 3, 6, 5, 4.

PRNG Tests Using the Now Superseded FIPS 140-1 by James Pate Williams, Jr., BA, BS, MSwE, PhD

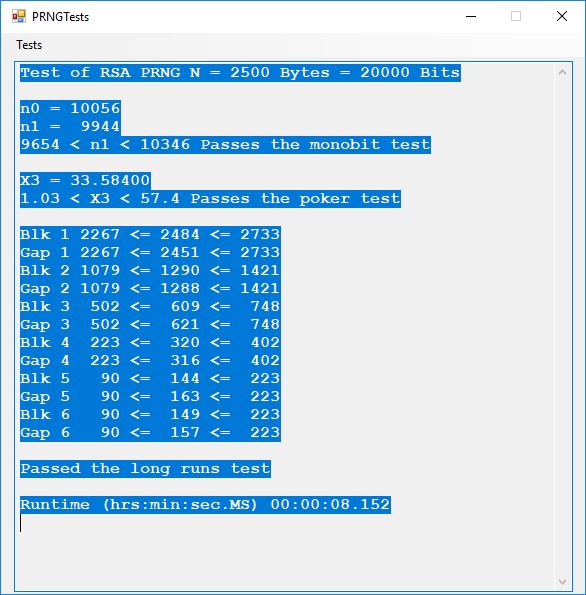
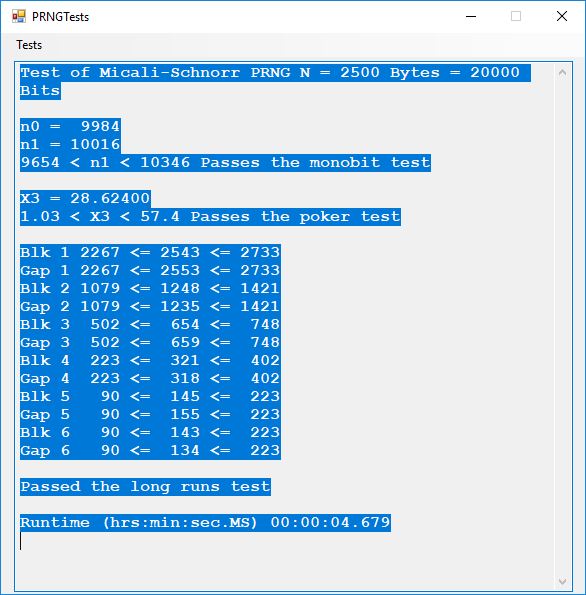
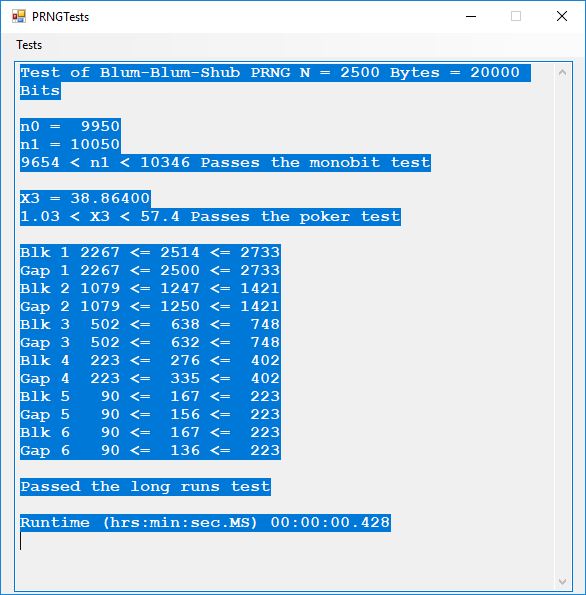
This blog post is dedicated to Section 5.3.1 ANSI X9.17 generator page 173 with 5.11 Algorithm and Section 5.4.4 Five basic tests pages 181-183 especially 5.32 Note of the Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone. I developed a PRNG test program for three PRNGs namely, Triple-AES, Triple-DES, and the C# built-in PRNG.

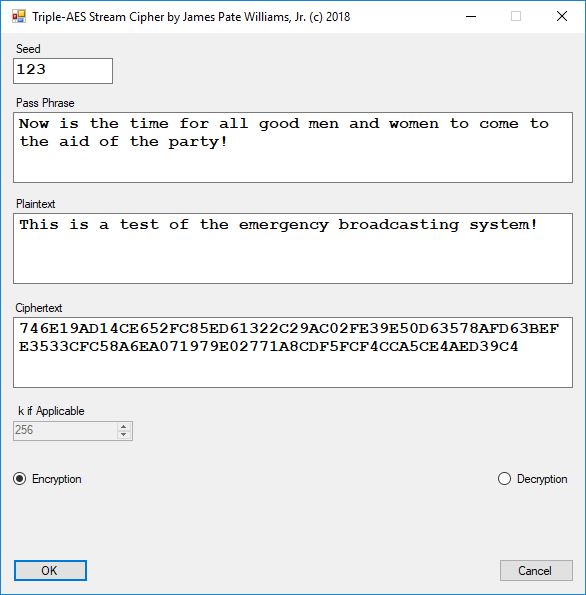
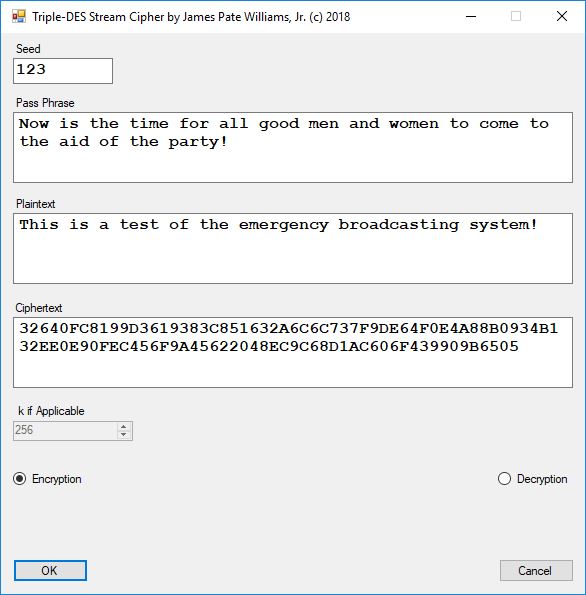
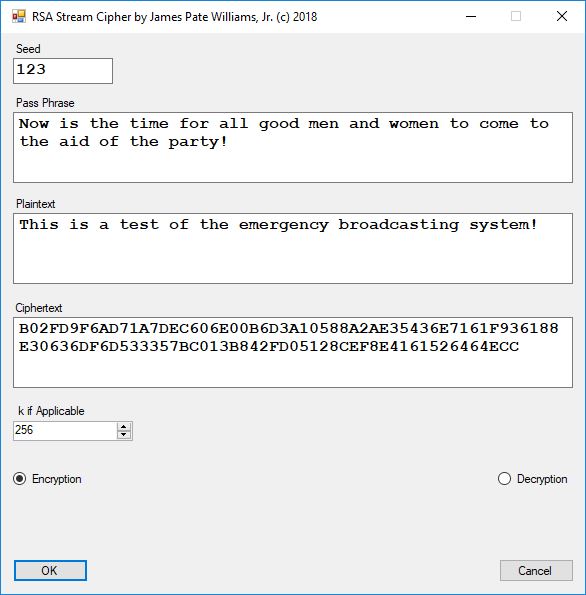
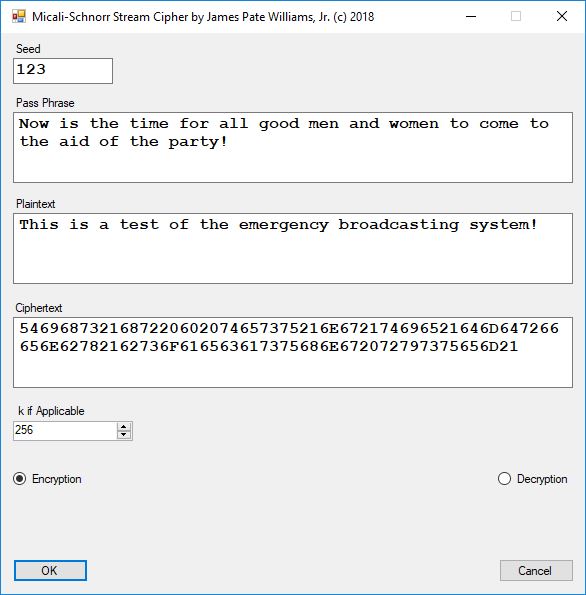
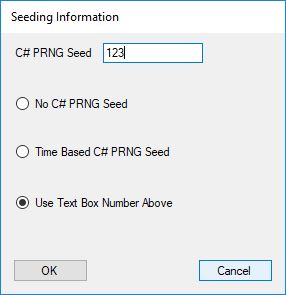
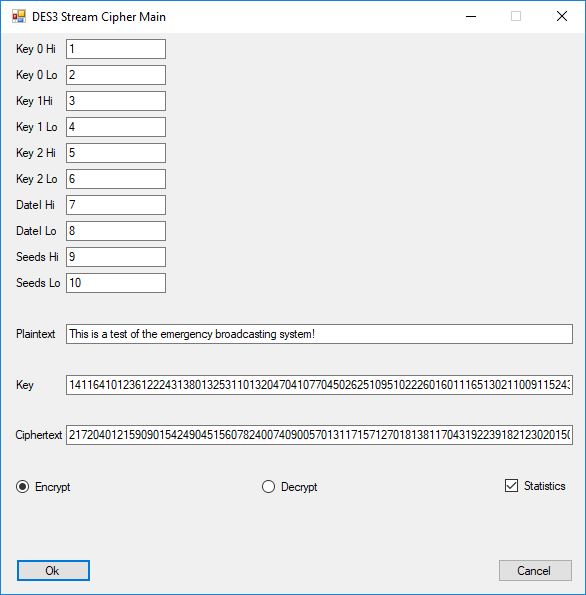
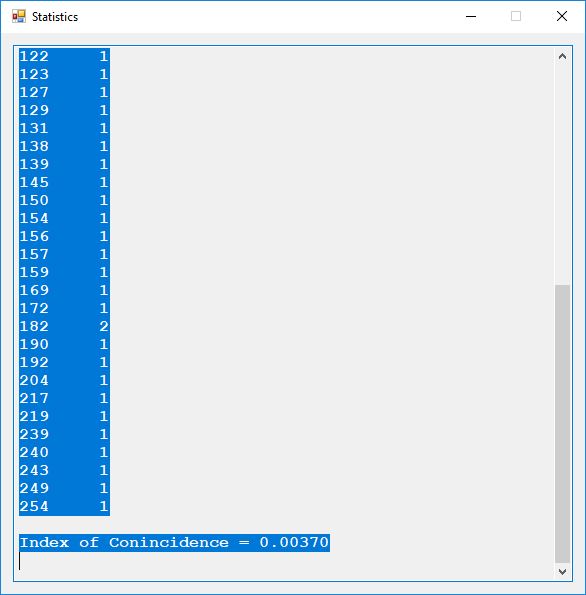
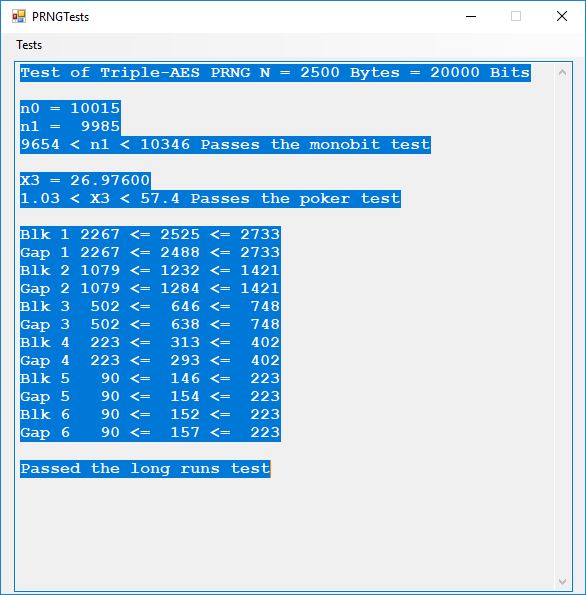
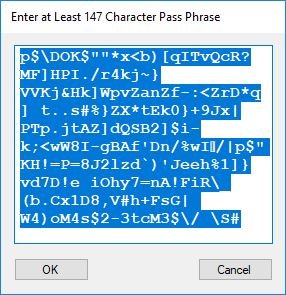
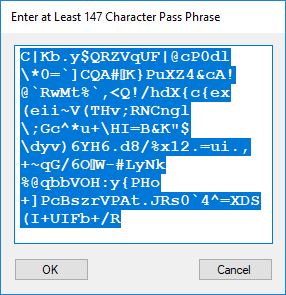
Each time an algorithm is run a randomly generated key is generated based on the time of day and the C# built-in PRNG with a key space of 2147483647 possible seeds. Triple-AES requires a 147 7-bit ASCII key and part of a similar key is used to construct the 296-bit Triple-DES key material. Now onto my C# Windows Forms application’s screenshots.

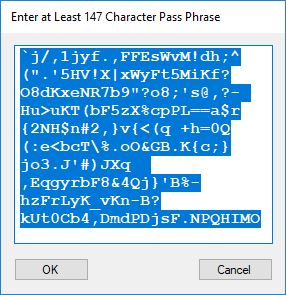
PRNGTests AES Key

PRNG Tests AES

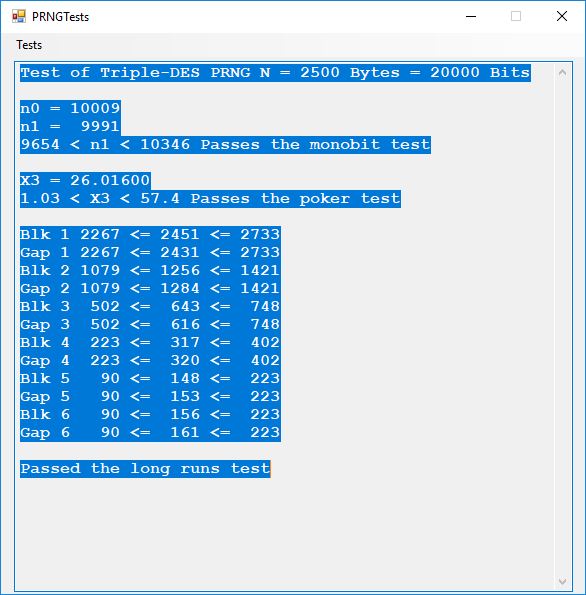
PRNG Tests DES Key

PRNG Tests DES

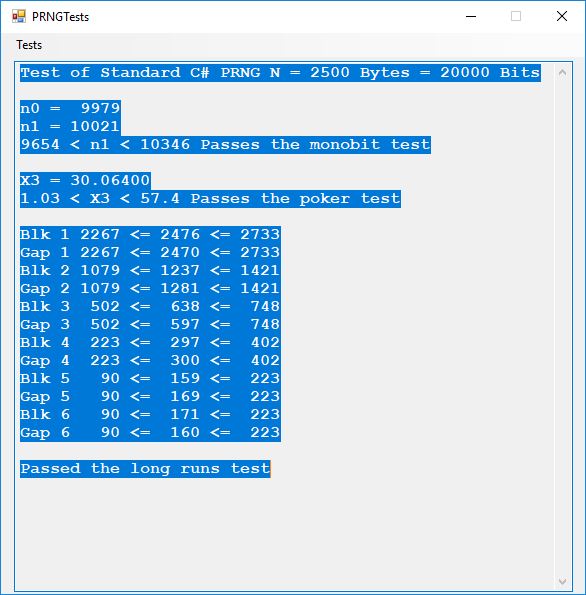
PRNG Tests C#

PRNG Tests Other AES

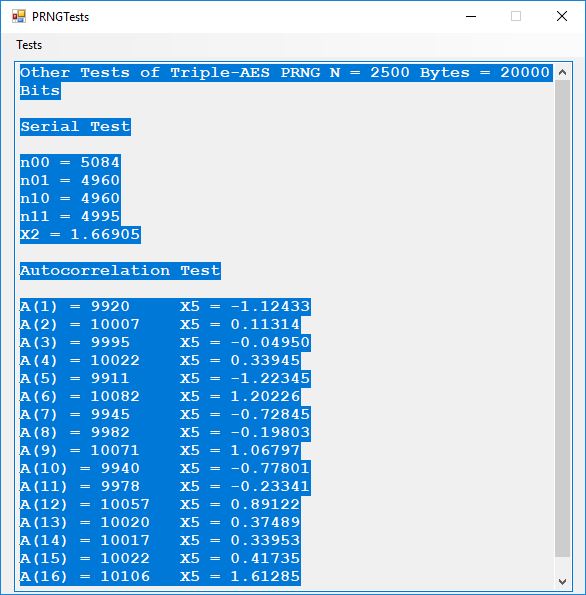
PRNG Tests Other AES Data

PRNG Tests Other DES Key

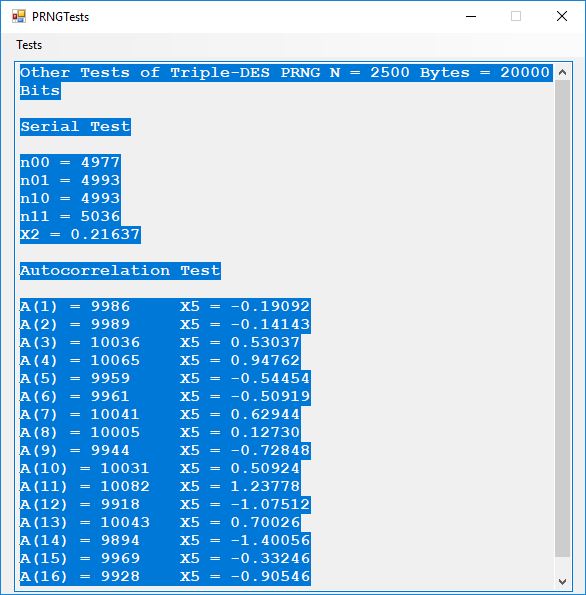
PRNG Tests Other DES Data

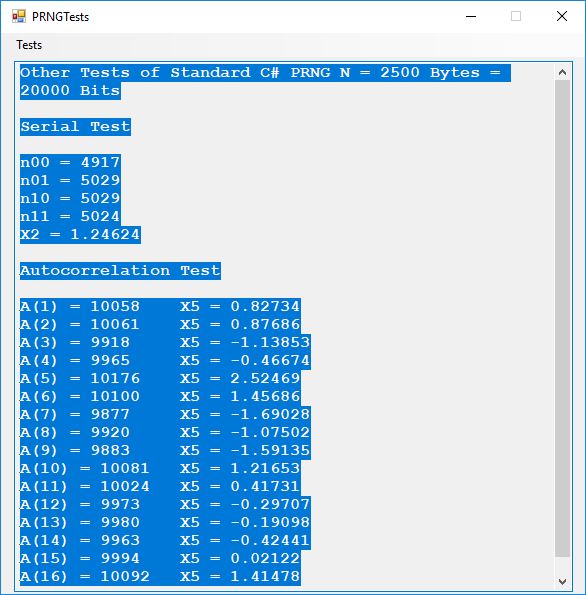
PRNG Tests Other C#

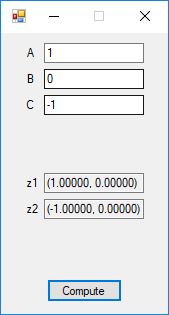
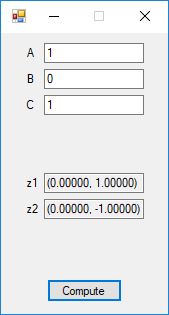
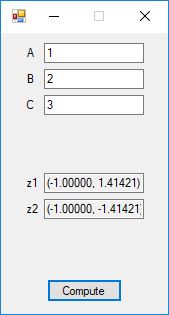
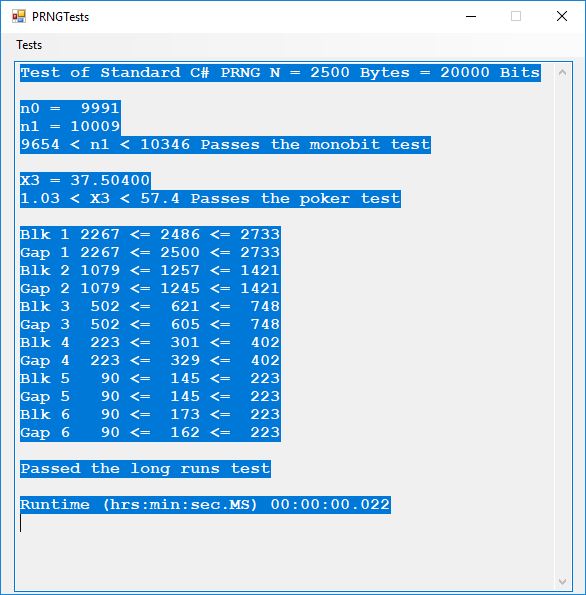
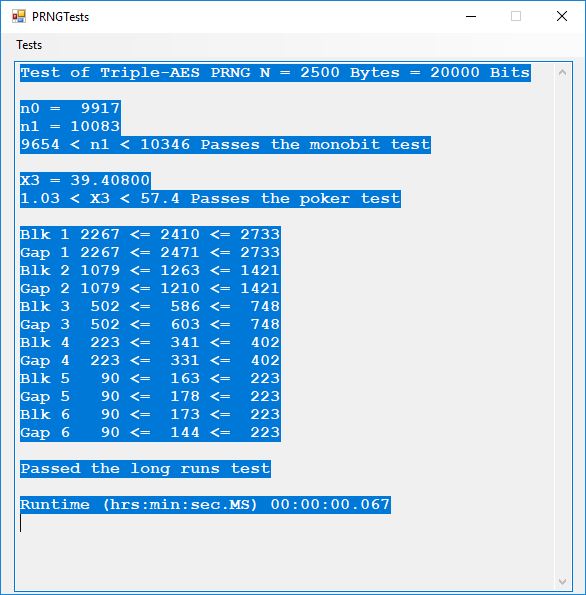
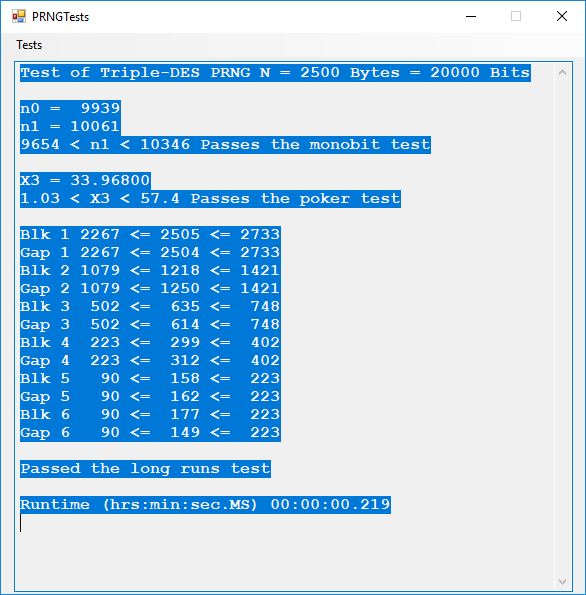
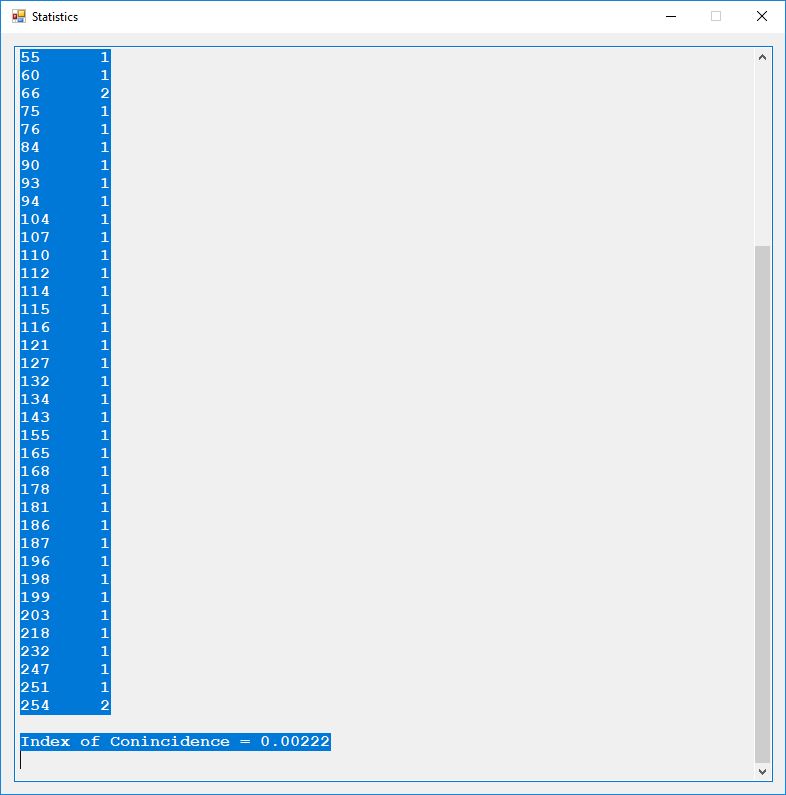
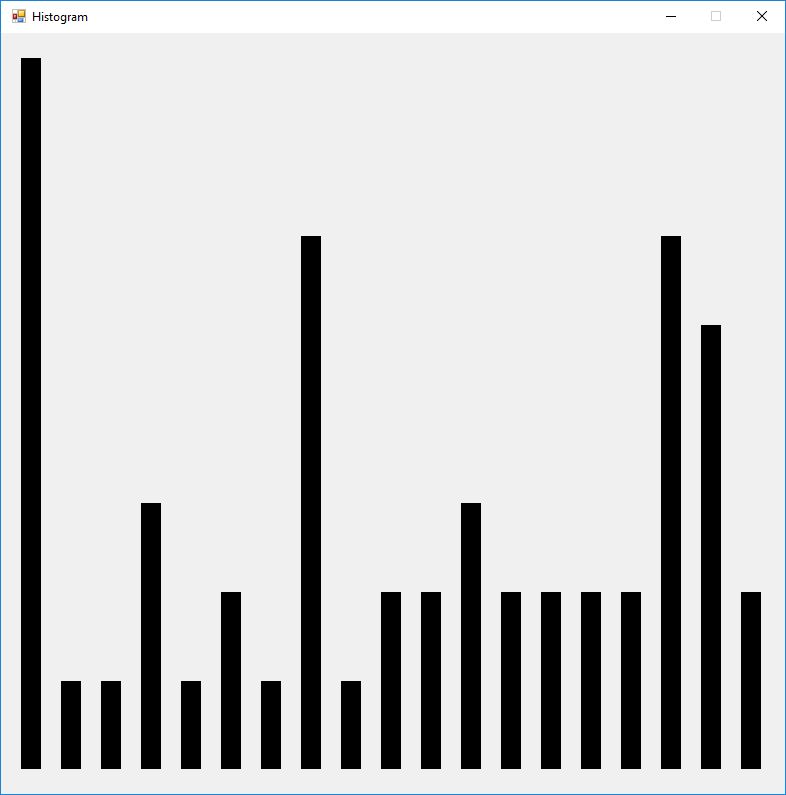
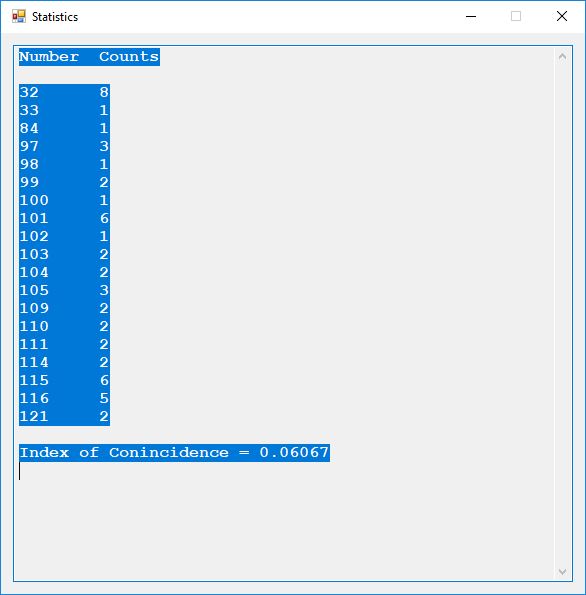
We use the five basic statistical tests of Chapter 5 Section 5.4.4 which are as follows:

Monobit Test also Known as the Single Bit Frequency Test
Serial Test also as the Two-Bit Frequency of Occurrence Test
Poker Test
Runs Test (Not to be confused with Montezuma’s Revenge)
Autocorrelation Test

Below is a copy of a recent email of mine concerning Secret Key Exchange or Distribution:

The linchpin and point of greatest vulnerability in any secret key cryptographic system is the key exchange mechanism. Now suppose that we are living in a post quantum computer world. This means that traditional public key cryptosystems such as RSA (integer factorization problem based) and elliptic curve public key cryptography (discrete logarithm problem based) are effectively broken. That implies that any public key based cryptographic key exchange is compromised over communication channels where Eve, the classical eavesdropper, is listening in on the key exchange between Alice and Bob. Quantum cryptography over fiber optic channels allows the communication endpoints to detect the eavesdropper and thus abort a potentially compromised key exchange. However, quantum cryptography is not readily available everywhere on the vast Internet. The rest of this email missive is devoted to other more exotic means of secret key exchange.

Human to human key exchange is optimal provided that all human beings in the loop are trustworthy. A good way to exchange secret keys is via a diplomatic courier with a diplomatic pouch and the key bits are concealed by a steganographic means.

Now suppose an adversary of an English speaking and reading country has two agents or human intelligence operatives that have infiltrated the country. Further both agents have the same 1024-bit seeded pseudorandom number generator-based stream cipher on their desktops and/or laptops for secure communications. That means they must somehow pass 147 secret 7-bit printable ASCII characters of information between one another for each quasi-one-time pad message. Each character represents 7 bits of the key and there are 5 bits left over after construction of each key. Also, suppose an actual face-to-face meeting between the two spies is inadvisable. Enter the text based social media or library book code. Now suppose the two spies are connected to one another via Facebook but are afraid to use text messaging for direct key exchange or clandestine communication. The solution is to use a shared Facebook page of text to construct the secret key. One spy shares a Facebook post containing at least 147 English characters and the other spy looks up the post. Both spies cut and paste the first 147 English characters of the post into a key constructing application. Voila, now both spies can communicate using their handy dandy stream cipher and email and/or cell phone text messaging of encrypted data in the form of three-digit decimal numbers. An alternative key exchange could be by the classic and readily available book code. Assume both spies have access to the same library, but not concurrent access. Both somehow agree to go and copy 147 characters from the same book in the library’s reference section. They write down the passage and take it home to enter the text into the key generator. Again, we have a means of clandestine key exchange.

Triple-AES Stream Cipher Using the ANSI X9.17 Pseudorandom Number Generator (PRNG) by James Pate Williams, Jr. BA, BS, MSwE, PhD

The Advanced Encryption Standard (AES) is fully described in the National Institute of Standards and Technology (NIST) publication:

Click to access NIST.FIPS.197.pdf

AES is a secret key block cipher with a block length of 128-bits and variable key lengths of 128-bits, 192-bits, and 256-bits.

The ANSI X9.17 pseudorandom number generator is described by Alfred J. Menezes, ET AL. in the Handbook of Applied Cryptography on page 176 5.11 Algorithm.

We use triple-AES with three 256-bit keys in Encryption-Decryption-Encryption mode. Also we utilize two 128-bit numbers. The total key space is (768 + 256)-bits = 1024-bits.

We now illustrate in the following screenshots our C# implementation of a stream cipher using the preceding algorithms.

We use the following dialog to allow under certain circumstances the application to randomly generate the seed material for our PRNG. Unfortunately, the built-in C# PRNG only has 2^31 -1 = 2147483647 different seeds. This cuts down on the amount of thought and typing required but is inherently dangerous due to the relatively small number of seeds. If you want true security the requisite sixteen 64-bit numbers must be random.

AES3 Stream Cipher 0

AES3 Stream Cipher 1

AES3 Stream Cipher Encrypt 0

AES3 Stream Cipher Encrypt 1

AES3 Stream Cipher Decrypt 0

AES3 Stream Cipher Decrypt 1

Optimally we would like to 0 index of coincidence, but 0.00222 is reasonably acceptable.

ANSIX9_17 Source Code

Triple-DES Stream Cipher Using the ANSI X9.17 Pseudorandom Number Generator (PRNG) by James Pate Williams, Jr. BA, BS, MSwE, PhD

In this blog post we give some information about my implementation of a C# triple-DES stream cipher using the ANSI X9.17 pseudorandom number generator of 5.11 Algorithm in the Handbook of Applied Cryptography by Alfred J. Menezes, ET AL. page 173. This is about as close as I can come to a one time pad (perfect security) utilizing a triple-DES based function for key generation. I suspect the security is pretty tight as long as one does not stupidly reuse a key. Recall from my previous blogs on the ANSI X9.17 matrix cipher that key space is 168-bits for triple-DES in E-D-E mode and an additional 128-bits in other key parameters for a total of 296-bits.

DES3 SC Encrypt

DES3 SC Encrypt Histogram

DES3 SC Encrypt Statistics

DES3 SC Decrypt Histogram

DES3 SC Decrypt Statistics

It would be nice if the index of coincidence was 0, but this index is probably satisfactory.

Some Statistics for Another Matrix Cipher by James Pate Williams, Jr. BA, BS, MSwE, PhD

We first encipher the string “This is a test of the emergency broadcasting system!” which is a English language sample of length 52 ASCII characters.

New Matrix Cipher Encrypt 0

Below is a histogram of the plaintext characters.

New Matrix Cipher Encrypt 1

Here are the counts of the different plaintext characters and the statistic known as the index of coincidence. English has an index of coincidence of approximately 0.065, so this short sample is in that ballpark at 0.06067.

New Matrix Cipher Encrypt 2

Next we display part of the key material (upper triangular matrix elements), the ASCII encoded plaintext and the last column is the resulting ciphertext.

New Matrix Cipher Encrypt 3

We now display a histogram of the ciphertext.

New Matrix Cipher Decrypt 1

New Matrix Cipher Decrypt 2

The index of coincidence is 0. Each of the 52 plaintext characters map to a different ciphertext number in the range 2 to 977 inclusive. Now we show the decryption matrix, ciphertext, and plaintext.

New Matrix Cipher Decrypt 3

We now say a few more words about the cryptanalysis of this matrix cipher. Since the PRNG has a large key space, a direct brute force attack on the PRNG would probably be futile in a milieu without a quantum computer. We can guess values of N and we know that key matrix inverse has n * (n + 1) / 2 elements instead of n * n elements since it is an upper triangular matrix. In our sample the key matrix inverse has 52 * 53 / 2 = 26 * 53 = 1,378 matrix elements. Each matrix element is in the inclusive range 0 to 996 or 997 values. So we would need to brute force test N * n * (n + 1) / 2 possible key matrix inverses. In our case the number is 997 * 1,378 = 1,373,866 which is not a very large number by cryptanalytic standards but how many of those decryptions would make perfectly good sense? A reasonably adept adversary would not reuse the PRNG key and N for a new 52 ASCII character string so each message would require a new cryptanalytic attack.

Using the upper triangular nature of the key matrix inverse and a further assumption that the plaintext is in the range 32 to 127 or 96 different values, we can reduce the brute force attack to 96 * 1,378 = 132,288 possibilities. Again the adversary could somewhat thwart these cryptanalytic efforts by choosing a much larger N and n.

However, all of this mental masturbation amounts to a mute point since no modern and sane adversary would utilize such an easy cipher to break. Just use a one time pad based on the ANSI X9.17 PRNG utilizing triple-AES instead of triple-DES with three 256-bit E-D-E keys or an astounding 768-bits of key material for the cipher core alone plus 256 bits in additional secret information. The final keyspace of such a scheme would be 1024-bits!

Another Matrix Cipher by James Pate Williams, Jr. BA, BS, MSwE, PhD

This is perhaps an improvement on the matrix cipher of a previous blog post of mine. In that post I introduced a matrix cipher whose keys were generated by selection of a seed such that 1 <= seed <= 2147483647, a number N such that 2 <= N <= 1000, and plaintext of length n such that 1 <= n <= N -1.

This matrix cipher relies on the ANSI X9.17 pseudorandom number generator (PRNG) of 5.11 Algorithm of the Handbook of Applied Cryptography by Alfred J. Menezes, et al. The PRNG uses triple-DES with a potential 168-bit (56 * 3 = 168) key space using E-D-E (Encryption key 1 – Decryption key 2 – Encryption key 3). Also, a 64-bit date related number and a 64-bit random seed are needed to initialize the PRNG.

The key space for the algorithm is (168 + 128) bits which is 296 bits. Here is the encryption and decryption of the ASCII ten characters string “ATTACK NOW”.

New Matrix Cipher 0

New Matrix Cipher 1

New Matrix Cipher 2

New Matrix Cipher 3

New Matrix Cipher 4

The first step in the cryptanalysis of this cipher would be to determine the modulus of the matrix and vector calculations N. I don’t know how many ciphertexts would be necessary to perform this task. From the preceding known ciphertext we find that N is at least 991. From traffic analysis we may have determined that the maximum value of N is 1000. That means would we only need to try 10 values of N.

A Matrix Cipher by James Pate Williams, Jr., BA, BS, MSwE, PhD

Suppose you have a n vector of ASCII encoded characters, arbitrarily choose 1 <= n <= 1000. Choose a modulus N such that 128 <= N <= 1000. Also choose a pseudo-random number seed 1 <= s <= 2147483647. Next find a random n x n matrix that is invertible by Gaussian elimination over the integer field consisting of N elements. Suppose this matrix is M and its tridiagonal form is M’. Now suppose the plaintext is the n vector P and the ciphertext is the n vector C then we have for encryption:

C = M’P

Further assume the inverse of M’ is N’. For decryption we use the equation:

P = N’C

Where

M’N’ = N’M’ = I

Such that I is the n x n identity matrix.

This cipher is related to the classic Hill Cipher. This cipher is polyalphabetic. We show the results of one encryption and decryption using 10 ASCII ‘A’ characters, N = 999, and s = 1. As you can see each occurrence of the letter ‘A’ which is encoded as the decimal number 65 leads to different integer in the range 0 to 998 which has a maximum of 10 bits. The key consists of the 100 integers in the original 10 x 10 matrix. The application was implemented in C# using a Gaussian elimination over a number field algorithm from Henri Cohen’s A Course in Computational Algebraic Number Theory.

Matrix Cipher 0

Matrix Cipher 1

Matrix Cipher 2

Two of My Many Sorting Algorithms Implementations by James Pate Williams, Jr. BA, BS, MSwE, PhD

A recurring theme in my life has been to implement and re-implement the sorting algorithms found in Harold Lorin’s treatise Sorting and Sort Systems and Thomas H. Corman et al.’s Algorithms. I purchased a copy of Lorin’s book in the summer of 1979 and Corman’s textbook in 1999 or 2000. This has been good exercise in translating from one computer language to a later and greater newer computer language. I began in BASIC and FORTRAN IV and transitioned to C, C++, C#, Common LISP, Java, Modula-2, Pascal, and Scheme in alphabetic not chronological order. In this blog we cover two C# applications, one from October 26, 2010, named Sorting Comparisons and the other from January 17, 2015, with the moniker Sorting.

In the Sorting Comparisons application, we compare the sorting algorithms: Heap Sort, Quick Sort, and Singleton’s Sort. The first two algorithms are from the Algorithms tome and Singleton’s Sort is from Lorin’s treatment. These are some of the fastest general purpose sorting algorithms available in my particular arsenal.

Sorting Comparisons Test All 16 Sorting Comparisons Time All 1000

Sorting Comparisons Source Code

https://code.msdn.microsoft.com/windowsdesktop/Tests-of-Six-Sorting-94aa6fd0?redir=0

Excerpt from My Memoirs “Clinging onto the Edge of the Abyss” by James Pate Williams, Jr. BA, BS, MSwE, PhD

I believe in late spring quarter of 1978, Mr. P.M. Hicks, a chemistry and physics professor at LaGrange College, introduced me to a large desktop Texas Instruments (TI) programmable calculator. I immediately became immersed in the manual and I learned the rudiments of calculator programming on this machine.

I advanced onto LaGrange College’s new Data General Eclipse minicomputer in the summer of 1978. I taught myself Dayton BASIC (Beginner’s All Purpose Symbolic Instruction Code) using the book “BASIC Programming” by Paul W. Murrill and Cecil L. Smith of which I still own a copy and it is copyrighted 1971. I seem to recall I special ordered the textbook from the LaGrange College library. This self-study put me many steps in front of my peers in the Fall Quarter of 1978 when I took a course under Professor Kenneth Cooper on BASIC programming. I taught Professor Cooper how to perform matrix and vector calculations using the Data General BASIC interpreter.

I also was taking my first course in physical chemistry in the fall of 1978. During the week of Monday, November 6, 1978 my physical chemistry partner Chuck H. Pitts (now Dr. Chuck H. Pitts, a prominent dentist in LaGrange, GA) did an experiment whose lab report title was “Determination of Molecular Size and Avogadro’s Number”. I seem to recall the division of labor was that I perform the calculations with the aid of a BASIC computer and Chuck and I would write up the experiment and I believe someone in the Callaway Foundation office or Chuck did the actual typing of the document at the Callaway Foundation office on Broome Street in LaGrange, GA. Well it took a lot of persuasion by Chuck to get me to do my part, since back in that era I was prone to destructive perfectionism. (Incidentally, I did not give up on being a perfectionist until Professor Felton at Georgia Tech in 1981 stated categorically “There is no room for perfectionism in science.”)

In the Winter Quarter of 1979 I took a FORTRAN (Formula Translator) IV course under Professor Kenneth Cooper. That quarter I also had Professor Cooper for Physical Chemistry II and Biochemistry. I did well in the computer programming course and I can remember helping several fellow students to pass the course. Professor Brooks Shelhorse then of the Math Department was one of my fellow classmates that I tutored. Biochemistry was an 8:00 AM course. I spent a lot of late nights in the computer lab, so I would sometimes fall asleep during the biochemistry lectures. I distinctly remember Dr. Cooper hurling an eraser near me to wake me up one morning. I made B’s in the two chemistry courses.

Spring Quarter of 1979 was my final quarter as a chemistry student at LaGrange College. I took Quantitative Analysis II, an Independent Study in Chemistry, General Physics III, and Angling. I made all A’s that quarter. The independent study was an introductory course to architecture and programming of the Intel 8085 microprocessor. Dr. Cooper in his time as a computer engineering student at Auburn University had built two very nice and unique computers, a rather large analog computer and a digital computer that consisted of an Intel 8085 microprocessor in a wooden box with hexadecimal keypad, two seven segment red light emitting diode displays, EEPROM, and RAM memory. I used the digital computer in my independent study. Professor Cooper taught me about the instruction set for the microprocessor and I would hand assemble my assembly language programs into two hexadecimal digit strings of machine code and manually enter the machine code via the keypad. One of my first assignments was to count down from 0xFF = 255 decimal to 0x00 = 0 decimal. I had a delay of about a ¼ second built into the program, so it took me one minute and four seconds to count down to zero. I was the only student in my independent study, therefore, it sometimes felt funny to have Professor Cooper give a whole one-hour lecture to an audience of one.

I bought the IBM book “Sorting and Sort Systems” by Harold Lorin in the summer of 1979. I proceeded to implement most of the sorting and merge algorithms in the book. I first translated the IBM PL/I (Programming Language I) code to BASIC and later for FORTRAN IV. Professor Cooper had developed a large BASIC program for the LaGrange College Registrar, Jimmy Herring. This program used a slow sorting algorithm which was either Shell sort of Bubble sort. I implemented a very fast sorting algorithm named Singleton’s sort in BASIC and was able to dramatically cut the time required to sort all the students by their Social Security Administration numbers which many colleges and universities then used as their primary flat-file or database key. I also began teaching myself the Data General Advanced Operating System (AOS) macro-assembly language. Like many computer programmers before I became infatuated with all the control over an operating system that assembly language afforded a knowledgeable programmer.

I convinced my parents to pay for me to audit Calculus and Analytic Geometry IV under Professor Shelhorse during the Fall Quarter of 1979, so I would have an excuse to be on campus to use my favorite computer, the LaGrange College Data General Eclipse minicomputer. That quarter I re-implemented my fast sorting algorithm in assembly language and set a new sorting time record with a program that sorting about 1000 student data records. Since the code was in AOS macro-assembly language it could not be readily integrated with the existing registrar’s system.

In 1980 I bummed around the college using the computer system until I was accepted to chemistry graduate school at the Georgia Institute of Technology for the Fall Quarter of 1980. I taught myself Data General Pascal and furthered my work with macro-assembly language, BASIC, and FORTRAN IV in the Winter, Spring, and Summer Quarters of 1980 at LaGrange College. I was unpaid computer programming teaching assistant for those three quarters which allowed me to earn my keep so to speak.

http://www.lagrange.edu/index.html

https://social.technet.microsoft.com/Profile/james%20pate%20williams%20jr

https://www.facebook.com/pg/JamesPateWilliamsJrConsultant/posts/

https://www.linkedin.com/in/james-williams-1a5b1370/